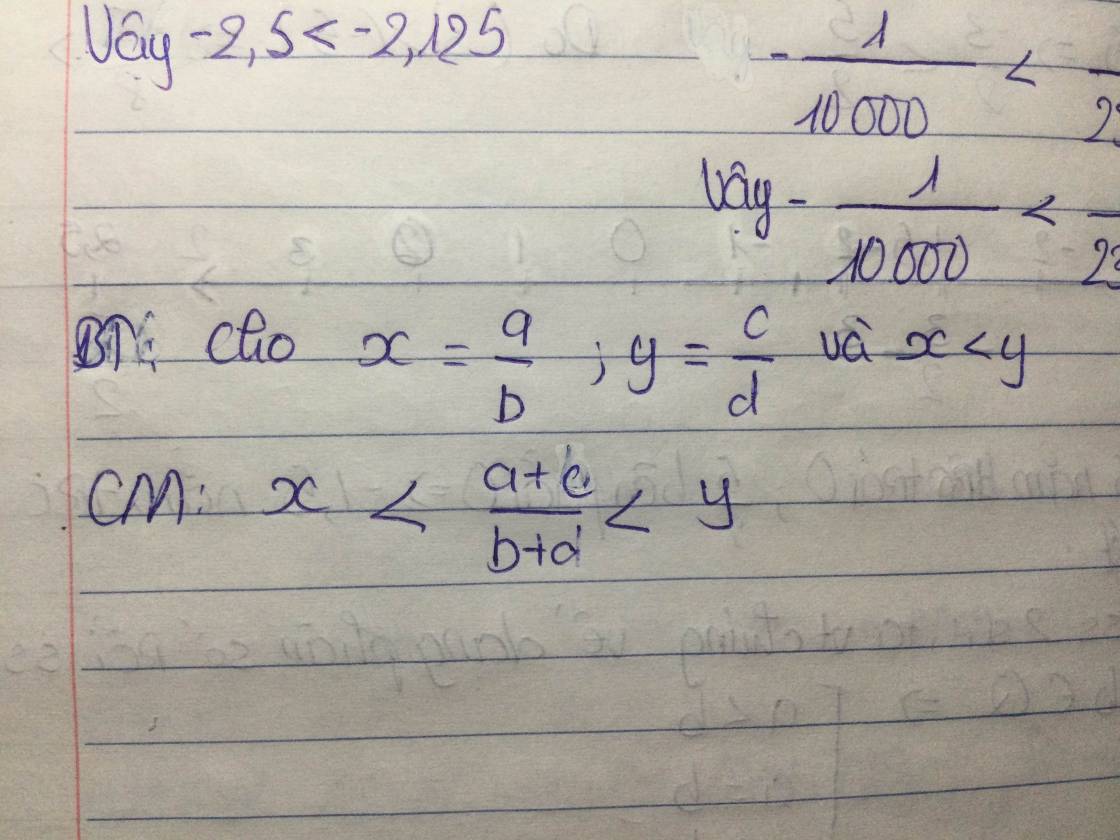Ta có:
\(x< y\)
\(\Rightarrow\dfrac{a}{b}< \dfrac{c}{d}\)
\(\Rightarrow ad< cb\)
Cộng 2 vế cho ab
\(\Rightarrow ad+ab< cb+ab\)
\(\Rightarrow a\left(b+d\right)< b\left(a+c\right)\)
\(\Rightarrow\dfrac{a}{b}< \dfrac{a+c}{b+d}\)
\(\Rightarrow x< \dfrac{a+b}{b+d}\left(1\right)\)
\(y>x\)
\(\Rightarrow\dfrac{c}{d}>\dfrac{a}{b}\)
\(\Rightarrow cb>ad\)
Cộng 2 vế cho cd:
\(\Rightarrow cb+cd>ad+cd\)
\(\Rightarrow c\left(b+d\right)>d\left(a+c\right)\)
\(\Rightarrow\dfrac{c}{d}>\dfrac{a+c}{b+d}\)
\(\Rightarrow y>\dfrac{a+b}{b+d}\left(2\right)\)
Từ (1) và (2)
\(\Rightarrow x< \dfrac{a+c}{b+d}< y\left(dpcm\right)\)
Đúng 2
Bình luận (0)
