Question

mn giúp mình với ạ

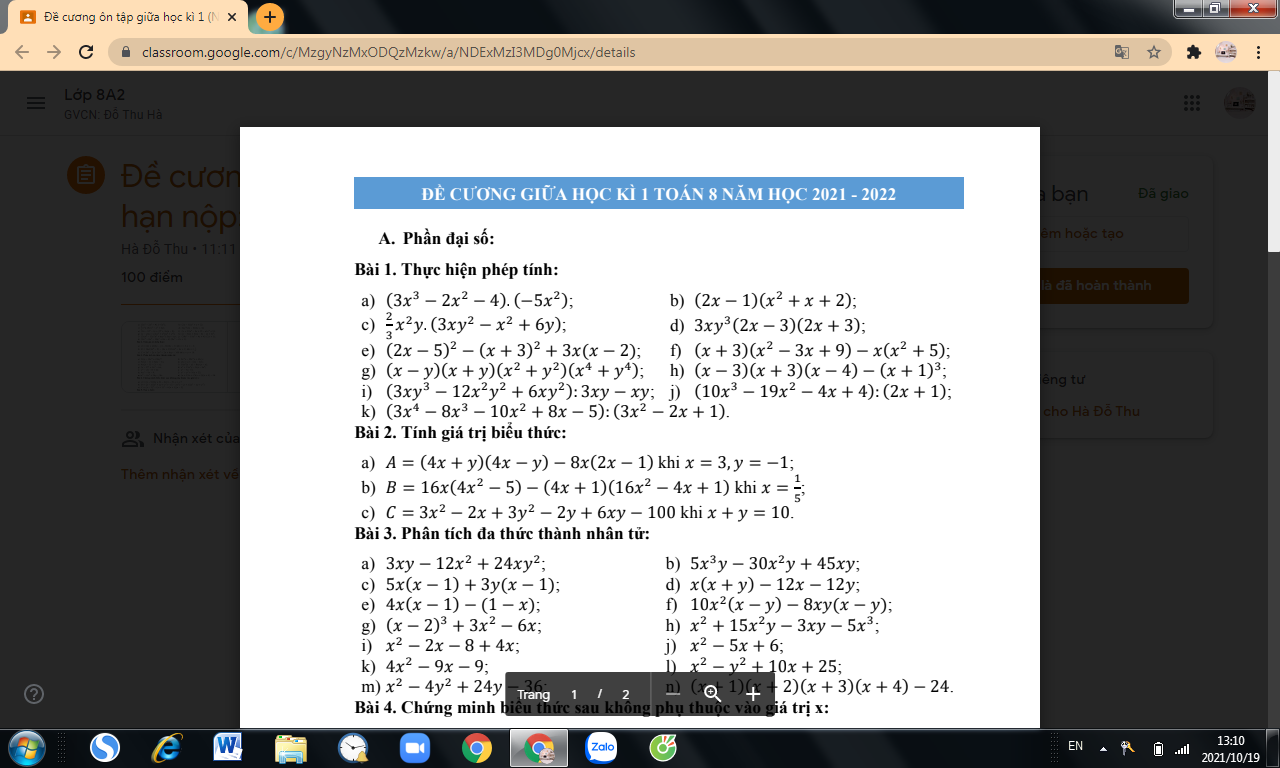
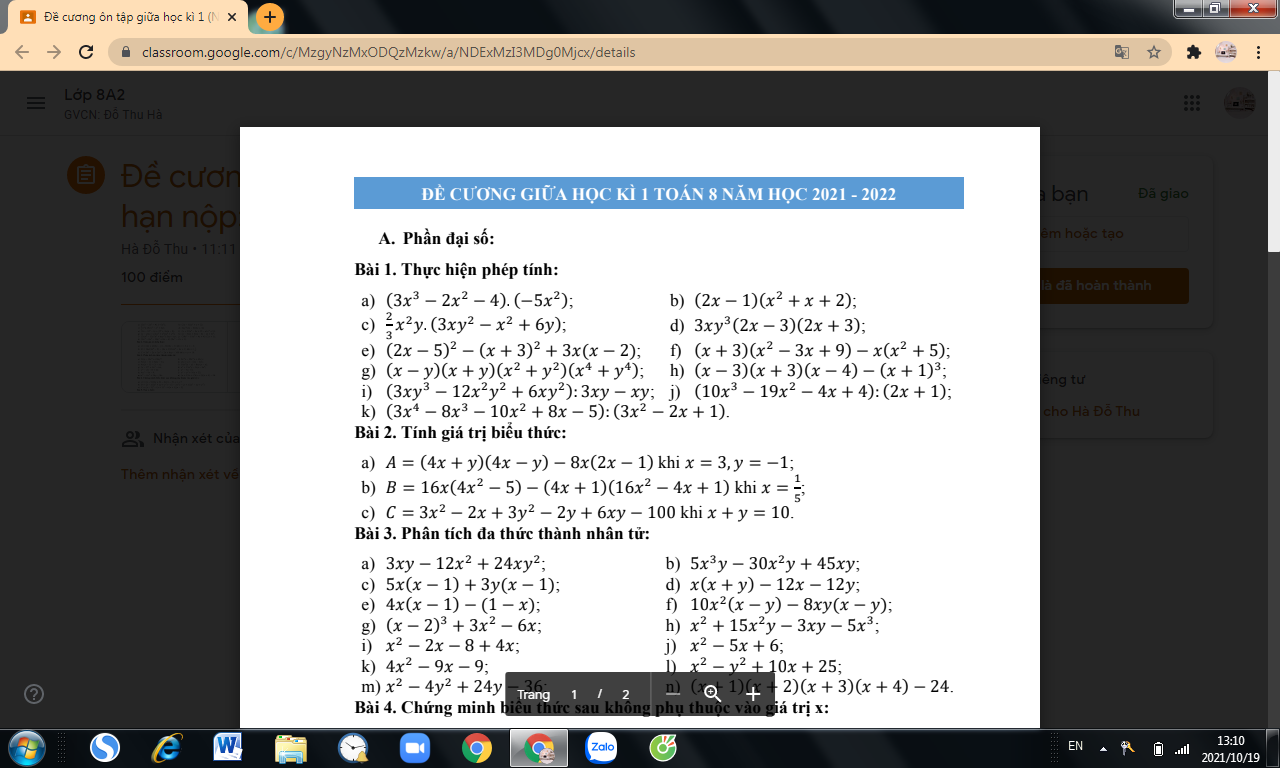
**Bài 2: (1,5 điểm)** Cho đường thẳng \( (d_1): y = 2x + 2 \) và \( (d_2): y = x - 3 \)
a) Tìm tọa độ giao điểm \( A \) của \( (d_1) \) và \( (d_2) \).
b) Cho đường thẳng \( (d_3): y = mx + 5 \). Tìm giá trị của \( m \) để ba đường thẳng \( (d_1), (d_2), (d_3) \) đồng quy tại một điểm.

**Bài 4: (3 điểm)** Cho tam giác \( ABC \) nhọn \( (AB < AC) \), hai đường cao \( AK \) và \( BE \) cắt nhau tại \( H \)
a. Chứng minh \( \triangle AKC \sim \triangle BEC \) từ đó suy ra \( CK \cdot CB = CA \cdot CE \).
b. Chứng minh: \( BE \cdot EH = EC \cdot AE \)
c. Kẻ \( CF \perp AB \), gọi \( N \) là giao điểm \( AK \) và \( FE \), \( D \) là giao điểm của đường thẳng \( BC \) và \( FE \). Gọi \( O, I \) lần lượt là trung điểm của \( BC \) và \( AH \). Chứng minh rằng \( ON \perp DI \).

Answer 1

Bài 2:

a: Phương trình hoành độ giao điểm là:

2x+2=x-3

=>2x-x=-3-2

=>x=-5

Khi x=-5 thì y=-5-3=-8

Vậy: Giao điểm là A(-5;-8)

b: Thay x=-5 và y=-8 vào y=mx+5, ta được:

\(m\cdot\left(-5\right)+5=-8\)

=>-5m=-8-5=-13

=>\(m=\frac{13}{5}\)

Bài 4:

a: Xét ΔCKA vuông tại K và ΔCEB vuông tại E có

\(\hat{KCA}\) chung

Do đó: ΔCKA~ΔCEB

=>\(\frac{CK}{CE}=\frac{CA}{CB}\)

=>\(CK\cdot CB=CE\cdot CA\)

b: Xét ΔEAH vuông tại E và ΔEBC vuông tại E có

\(\hat{EAH}=\hat{EBC}\left(=90^0-\hat{ACB}\right)\)

Do đó: ΔEAH~ΔEBC

=>\(\frac{EA}{EB}=\frac{EH}{EC}\)

=>\(EA\cdot EC=EB\cdot EH\)