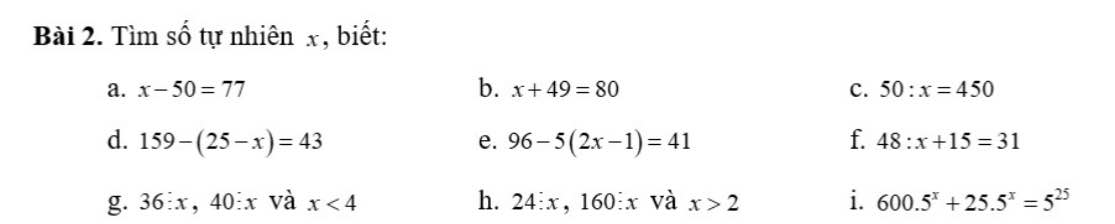\(=\dfrac{2^2-1+1}{\left(2-1\right)\left(2+1\right)}\cdot\dfrac{3^2-1+1}{\left(3-1\right)\left(3+1\right)}\cdot...\cdot\dfrac{\left(2020\right)^2-1+1}{\left(2020-1\right)\left(2020+1\right)}\)
\(=\dfrac{2}{1}\cdot\dfrac{3}{2}\cdot...\cdot\dfrac{2020}{2019}\cdot\dfrac{2}{3}\cdot\dfrac{3}{4}\cdot...\cdot\dfrac{2020}{2021}\)
\(=2020\cdot\dfrac{2}{2021}=\dfrac{4040}{2021}\)
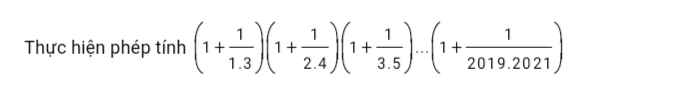
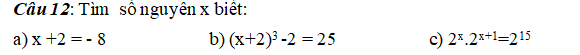
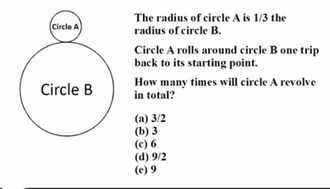mn giúp mik câu này với:
thật xin lỗi mn nhưng mn giúp mik câu hỏi này với!
1/2 x (x-2) + 1/3 (2-x) = x
MN ƠI GIÚP MIK CÂU NÀY VỚI AH
MIK CẢM ƠN!
Mn giúp mik với câu này là cô cho làm chơi thôi ai giải đc cho 200 Đ
xin lỗi mn nhưng giúp mik câu này đc ko ạ, mong mn giải chi tiết cho em! 
Mọi người ơi giúp mik câu này với Cho A=2+2^2+2^3+2^4+...+2^30 Chứng minh A chia hết cho 7.Mong đc mn giúp đỡ.☺
2^x : 2 = 16 mn giúp mik câu này nhé . cảm ơn mn nhiều nhoa
a) 6x : 2 = 16 ; b) 3^x-1 : 8 = 81 . Mn giúp mik câu này nhé . cảm ơn mn
Mn giúp mik bài này với ạ
Mn ơi Giúp mik bài này
86712 x 482947 = ?
Giúp mik với
