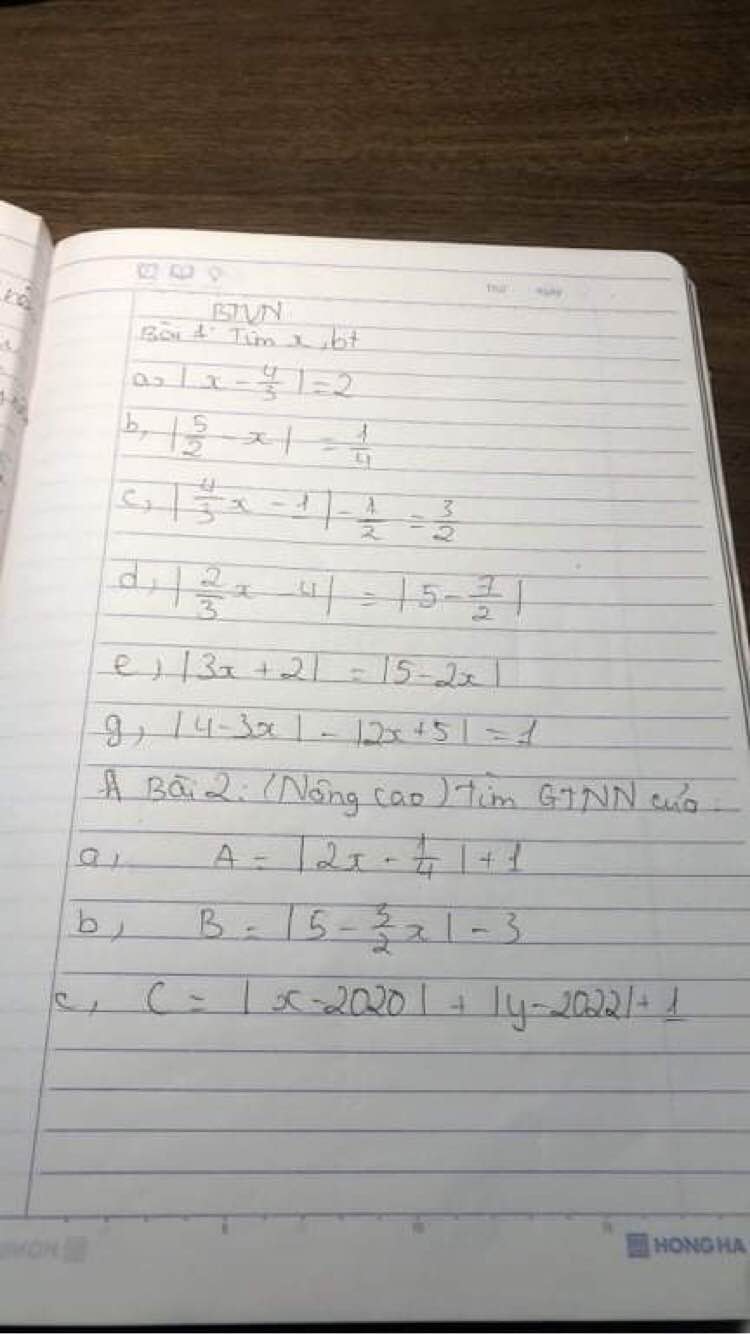a, \(\dfrac{x}{5}=\dfrac{y}{6};\dfrac{y}{8}=\dfrac{z}{11}\Rightarrow\dfrac{x}{40}=\dfrac{y}{48}=\dfrac{z}{66}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{40}=\dfrac{y}{48}=\dfrac{z}{66}=\dfrac{x+y-z}{40+48-66}=\dfrac{44}{22}=2\)
\(\Rightarrow x=80;y=96;z=132\)
b, Ta có : \(3x=8y\Leftrightarrow\dfrac{x}{8}=\dfrac{y}{3}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{8}=\dfrac{y}{3}=\dfrac{x-2y}{8-6}=\dfrac{4}{2}=2\Rightarrow x=16;y=6\)
a, Ta có: \(\dfrac{x}{5}=\dfrac{y}{6};\dfrac{ y}{8}=\dfrac{z}{11}\Rightarrow \dfrac{x}{40}=\dfrac{y}{48}=\dfrac{z}{66}\)
Và \(x+y-z=44\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{40}=\dfrac{y}{48}=\dfrac{z}{66}=\dfrac{x+y-z}{40+48-66}=\dfrac{44}{22}=2\\ \Rightarrow\left\{{}\begin{matrix}x=2.40\\y=2.48\\z=2.66\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=80\\y=96\\z=132\end{matrix}\right.\)
Vậy\(\left\{{}\begin{matrix}x=80\\y=96\\z=132\end{matrix}\right.\)
b, Ta có: \(3x=8y \Rightarrow \dfrac{x}{8}=\dfrac{y}{3}\)
Và \(x-2y=4\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{8}=\dfrac{y}{3}=\dfrac{x-2y}{8-6}=\dfrac{4}{2}=2\\ \Rightarrow\left\{{}\begin{matrix}x=2.8\\y=2.3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=16\\y=6\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}x=16\\y=6\end{matrix}\right.\)
a) Ta có: \(\dfrac{x}{5}=\dfrac{y}{6}\)
nên \(\dfrac{x}{20}=\dfrac{y}{24}\)(1)
Ta có: \(\dfrac{y}{8}=\dfrac{z}{11}\)
nên \(\dfrac{y}{24}=\dfrac{z}{33}\)(2)
Từ (1) và (2) suy ra \(\dfrac{x}{20}=\dfrac{y}{24}=\dfrac{z}{33}\)
mà x+y-z=44
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{20}=\dfrac{y}{24}=\dfrac{z}{33}=\dfrac{x+y-z}{20+24-33}=\dfrac{44}{11}=4\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{20}=4\\\dfrac{y}{24}=4\\\dfrac{z}{33}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=80\\y=96\\z=132\end{matrix}\right.\)
b) Ta có: 3x=8y
nên \(\dfrac{x}{\dfrac{1}{3}}=\dfrac{y}{\dfrac{1}{8}}\)
\(\Leftrightarrow\dfrac{x}{\dfrac{1}{3}}=\dfrac{2y}{\dfrac{1}{4}}\)
mà x-2y=4
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{1}{3}}=\dfrac{2y}{\dfrac{1}{4}}=\dfrac{x-2y}{\dfrac{1}{3}-\dfrac{1}{4}}=\dfrac{4}{\dfrac{1}{12}}=48\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{\dfrac{1}{3}}=48\\\dfrac{y}{\dfrac{1}{4}}=48\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=16\\y=12\end{matrix}\right.\)

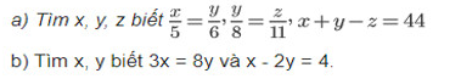










 giúp em vài bài này với em đang cần gấp ạ em cảm ơn mn rất nhiều ạ
giúp em vài bài này với em đang cần gấp ạ em cảm ơn mn rất nhiều ạ