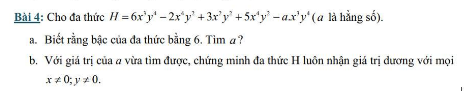a: \(H=6x^3y^4-2x^4y^2+3x^2y^2+5x^4y^2-a\cdot x^3y^4\)
\(=\left(6x^3y^4-a\cdot x^3y^4\right)+3x^2y^2+3x^4y^2\)
\(=x^3y^4\left(6-a\right)+3x^2y^2+3x^4y^2\)
Để bậc của đa thức H bằng 6 thì 6-a=0
=>a=6
b: Khi a=6 thì \(H=3x^2y^2+3x^4y^2\)
\(=3x^2y^2\left(x^2+1\right)\)
Khi x<>0 và y<>0 thì \(x^2>0;y^2>0;x^2+1>1>0\)
=>\(x^2\cdot y^2\left(x^2+1\right)>0\)
=>\(H=3\cdot x^2y^2\left(x^2+1\right)>0\forall x,y\ne0\)
Đúng 0
Bình luận (0)
