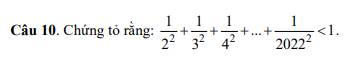Câu 5:
\(A=1+3+3^2+3^3+...+3^{19}+3^{20}\)
\(\Leftrightarrow3A=3+3^2+3^3+3^4+...+3^{20}+3^{21}\)
\(\Rightarrow3A-A=3^{21}-1\)
\(\Rightarrow2A=3^{21}-1\)
\(\Rightarrow A=\dfrac{3^{21}-1}{2}\)
Câu 3:
c: Trường hợp 1: n=2k
\(\Leftrightarrow n\left(n+2017\right)=2k\cdot\left(2k+2017\right)⋮2\)
Trường hợp 1: n=2k+1
\(\Leftrightarrow n\left(n+2017\right)=\left(2k+1\right)\left(2k+2018\right)⋮2\)
Câu 6:
\(S=1+9+9^2+...+9^{2017}\)
\(\Leftrightarrow9S=9+9^2+9^3+...+9^{2018}\)
\(\Rightarrow9S-S=9^{2018}-1\)
\(\Rightarrow8S=9^{2018}-1\)
\(\Leftrightarrow S=\dfrac{9^{2018}-1}{8}\)
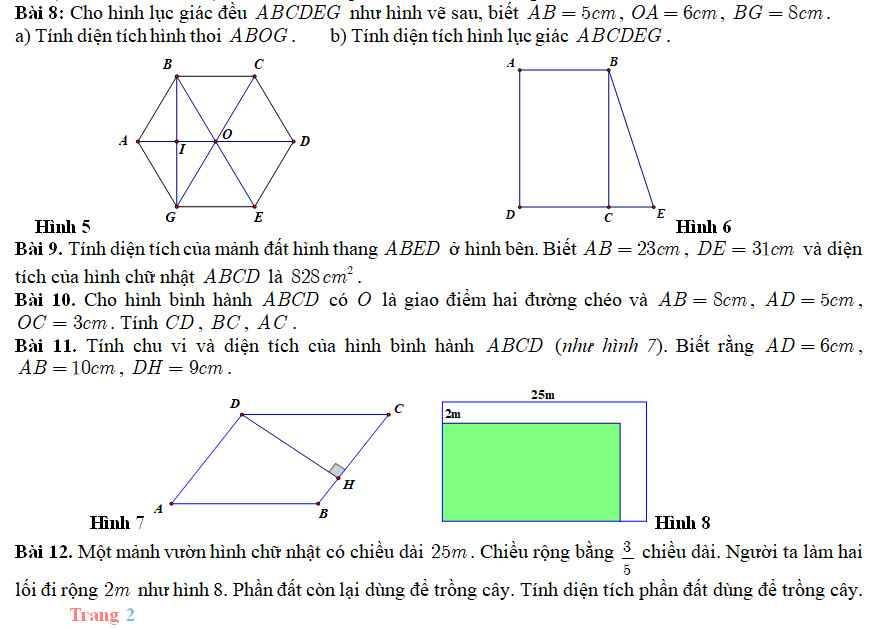chỉ giúp em mấy bài này với ạ em đng cần gấp ạ
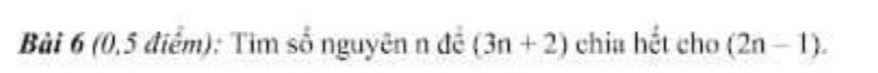mn giúp em với ạ, em đang cần gấp lắm ạ
