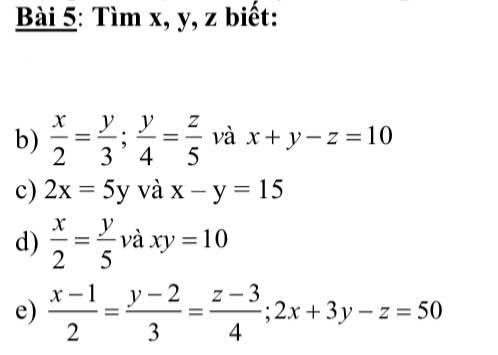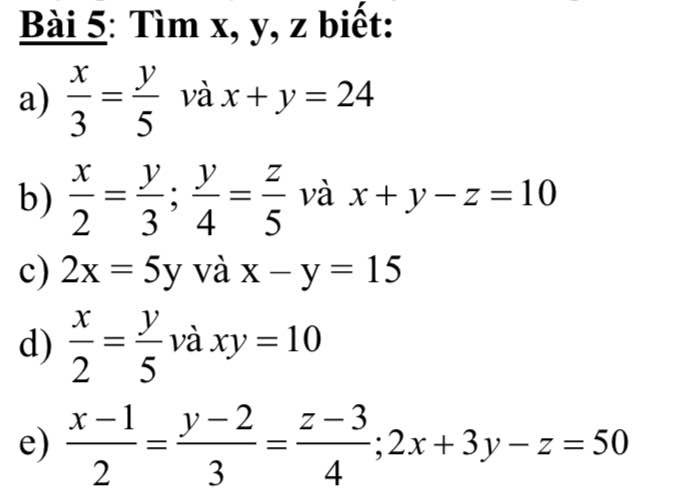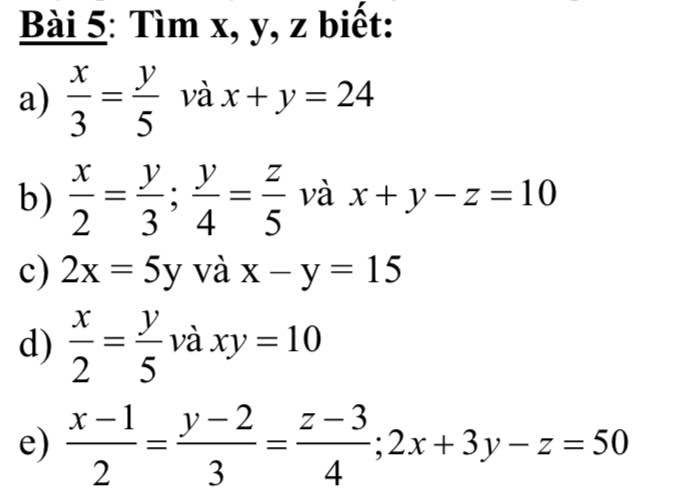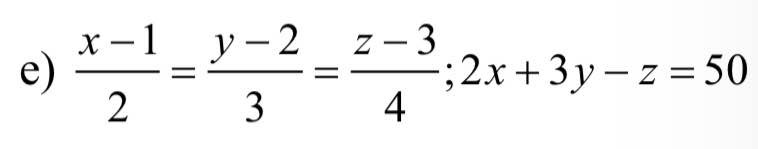\(b,\Rightarrow\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}=\dfrac{x+y-z}{8+12-15}=\dfrac{10}{5}=2\\ \Rightarrow\left\{{}\begin{matrix}x=16\\y=24\\z=30\end{matrix}\right.\\ c,\Rightarrow\dfrac{x}{5}=\dfrac{y}{2}=\dfrac{x-y}{5-2}=\dfrac{15}{3}=5\\ \Rightarrow\left\{{}\begin{matrix}x=25\\y=10\end{matrix}\right.\\ d,\text{Đặt }\dfrac{x}{2}=\dfrac{y}{5}=k\Rightarrow x=2k;y=5k\\ xy=10\Rightarrow10k^2=10\Rightarrow k^2=1\\ \Rightarrow\left[{}\begin{matrix}k=1\\k=-1\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=2;y=5\\x=-2;y=-5\end{matrix}\right.\)
\(e,\dfrac{x-1}{2}=\dfrac{y-2}{3}=\dfrac{z-3}{4}=\dfrac{2\left(x-1\right)+3\left(y-2\right)-z+3}{2\cdot2+3\cdot3-4}=\dfrac{2x+3y-z-2-6+3}{9}=\dfrac{45}{9}=5\\ \Rightarrow\left\{{}\begin{matrix}x-1=10\\y-2=15\\z-3=20\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=11\\y=17\\z=23\end{matrix}\right.\)
c: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{5}=\dfrac{y}{2}=\dfrac{x-y}{5-2}=5\)
Do đó: x=25; y=10