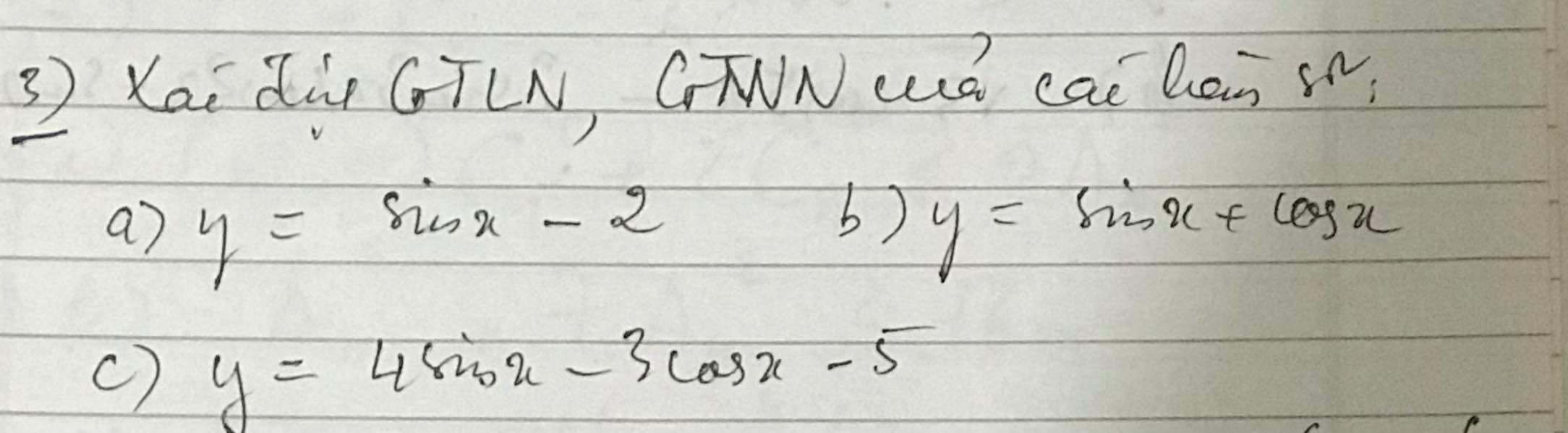c, Có thể giải theo hai cách tùy bạn nhé
Cách 1:
\(y=4sinx-3cosx-5=5\left(\dfrac{4}{5}sinx-\dfrac{3}{5}cosx\right)-5\\ \Rightarrow y=5.sin\left(x+\alpha\right)-5\)
Với \(\alpha\) thỏa mãn cos \(\alpha=\dfrac{4}{5};sin\alpha=\dfrac{3}{5}\)
\(\Rightarrow-1\le sin\left(x+\alpha\right)\le1\) \(\left(\forall x\in R\right)\)
\(\Leftrightarrow-5\le5sin\left(x+\alpha\right)\le5\left(\forall x\in R\right)\\ \Leftrightarrow-5-5\le5sin\left(x+\alpha\right)-5\le5-5\\ \Leftrightarrow-10\le5sin\left(x+\alpha\right)-5\le0\)
Vậy \(y_{max}=0;y_{min}=-10\)
Cách 2:
\(y=4sinx-3cosx-5\\ \Leftrightarrow4sinx-3cosx=y+5\)
Để phương trình trên có nghiệm
\(\Rightarrow4^2+\left(-3\right)^2\ge\left(y+5\right)^2\\\Leftrightarrow25\ge\left(y+5\right)^2\\ \Leftrightarrow-5\le y+5 \le5\\ \Leftrightarrow-10\le y\le0\)
Vậy \(y_{max}=-10;y_{min}=0\)
a, Ta có \(-1\le sinx\le1\Rightarrow-3\le y\le-1\)
Vậy gtln là -1 ; gtnn là -3
b, Ta có \(-1\le sinx\le1;-1\le cosx\le1\)
\(\Rightarrow-2\le sinx+cosx\le2\)
vậy gtln là 2;gtnn là -2
c, tương tự nhé