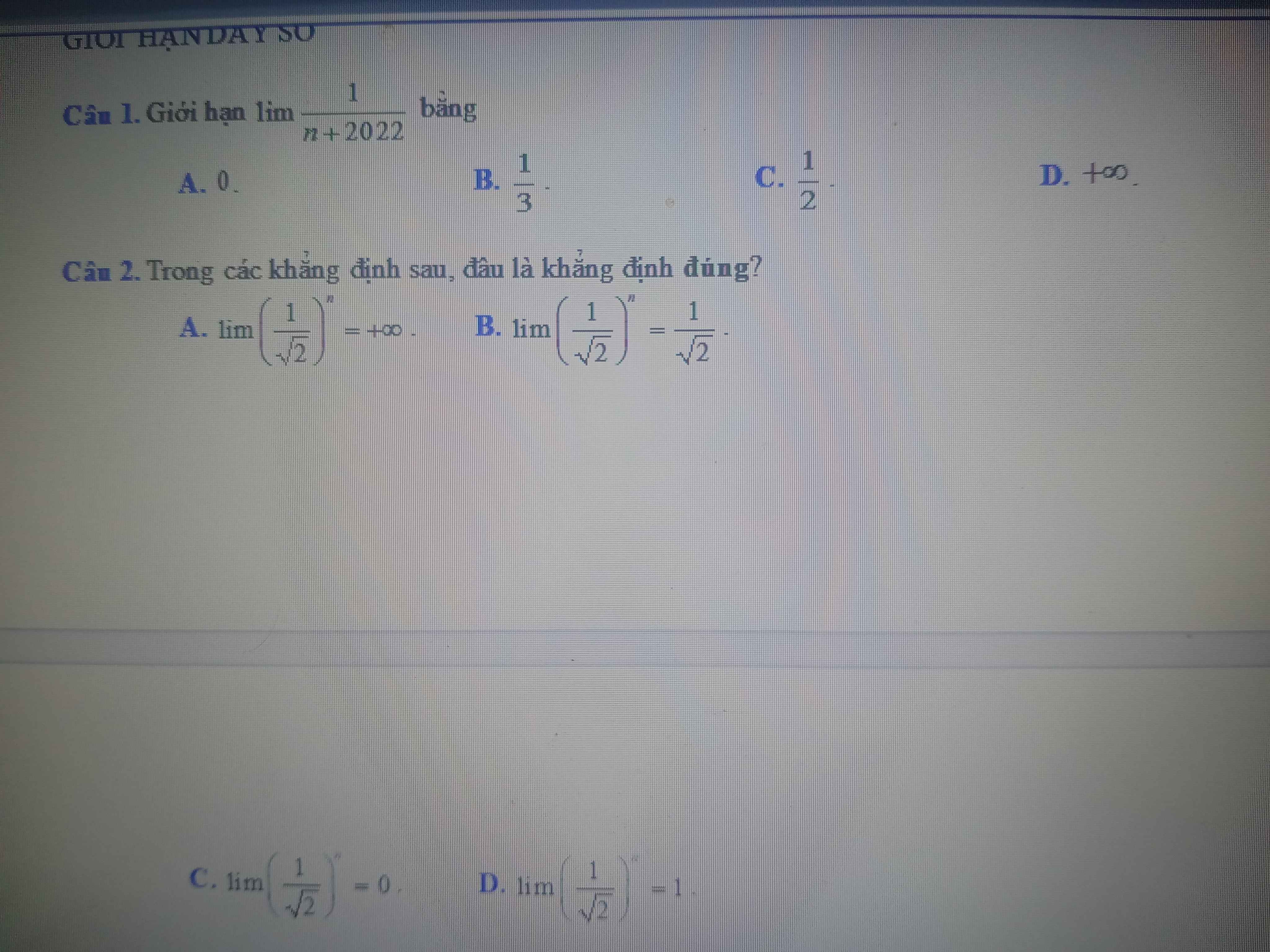
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
a)\(tanA+tanB+tanC=tanA+tanB-tan\left(A+B\right)=tanA+tanB-\dfrac{tanA+tanB}{1-tanAtanB}=\left(tanA+tanB\right).\dfrac{-tanAtanB}{1-tanAtanB}=-\dfrac{tanA+tanB}{1-tanAtanB}.tanAtanB=-tan\left(A+B\right)tanAtanB=tanCtanAtanB\)
b) \(tan\dfrac{A}{2}tan\dfrac{B}{2}+tan\dfrac{B}{2}tan\dfrac{C}{2}+tan\dfrac{C}{2}tan\dfrac{A}{2}=tan\dfrac{A}{2}tan\dfrac{B}{2}+tan\dfrac{C}{2}\left(tan\dfrac{A}{2}+tan\dfrac{B}{2}\right)=tan\dfrac{A}{2}tan\dfrac{B}{2}+cot\dfrac{A+B}{2}\left(tan\dfrac{A}{2}+tan\dfrac{B}{2}\right)=tan\dfrac{A}{2}tan\dfrac{B}{2}+\dfrac{1-tan\dfrac{A}{2}tan\dfrac{B}{2}}{tan\dfrac{A}{2}+tan\dfrac{B}{2}}\left(tan\dfrac{A}{2}+tan\dfrac{B}{2}\right)=1\)