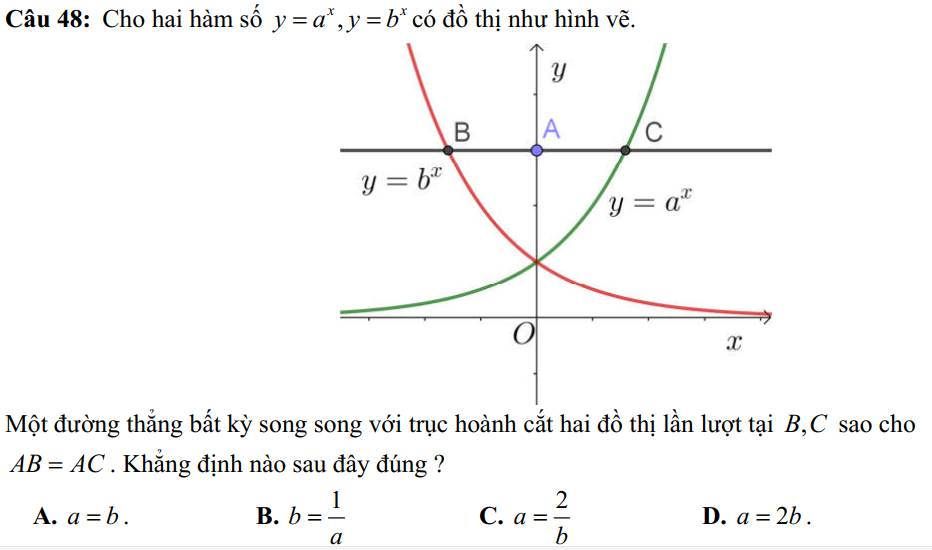
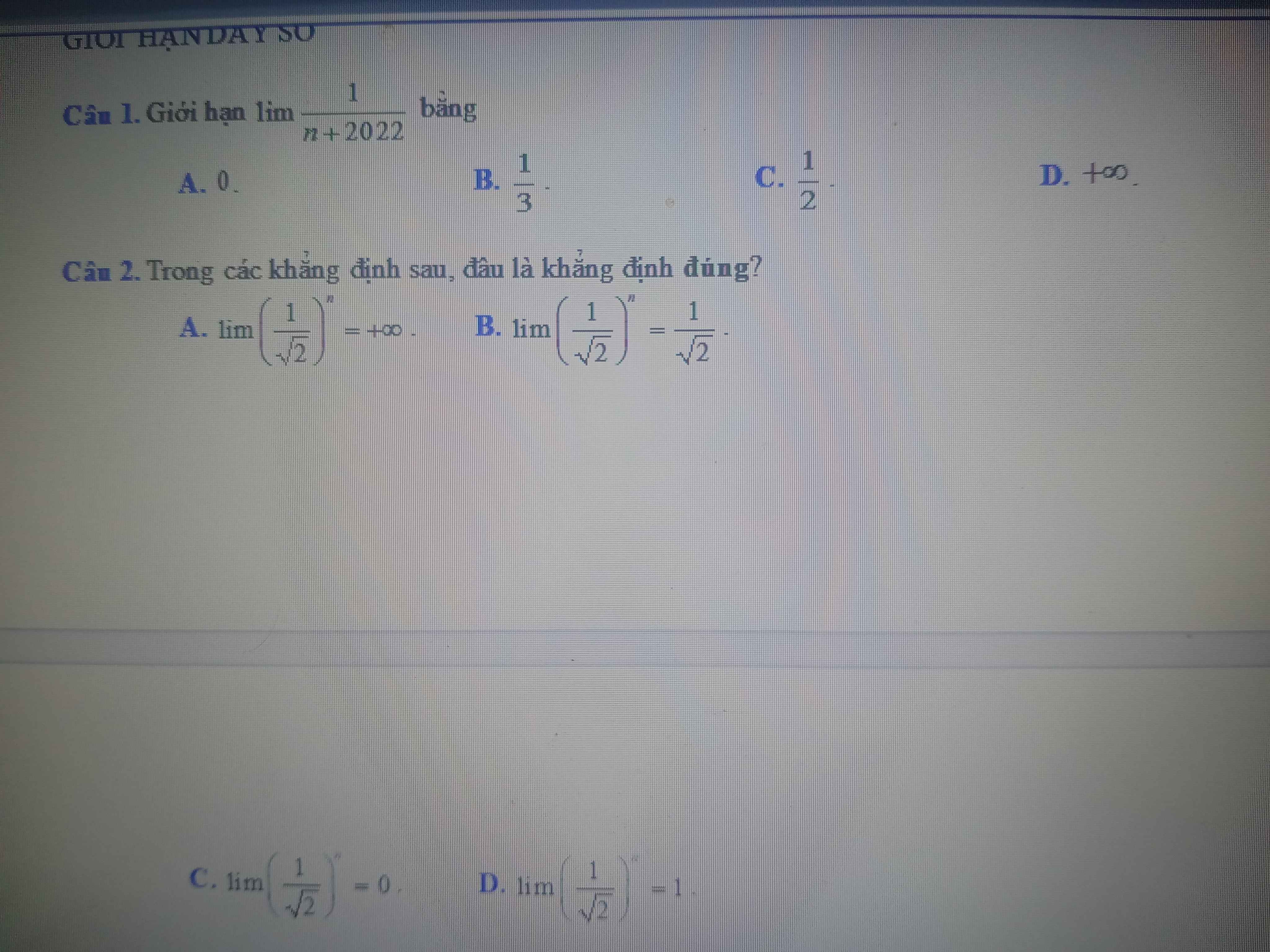
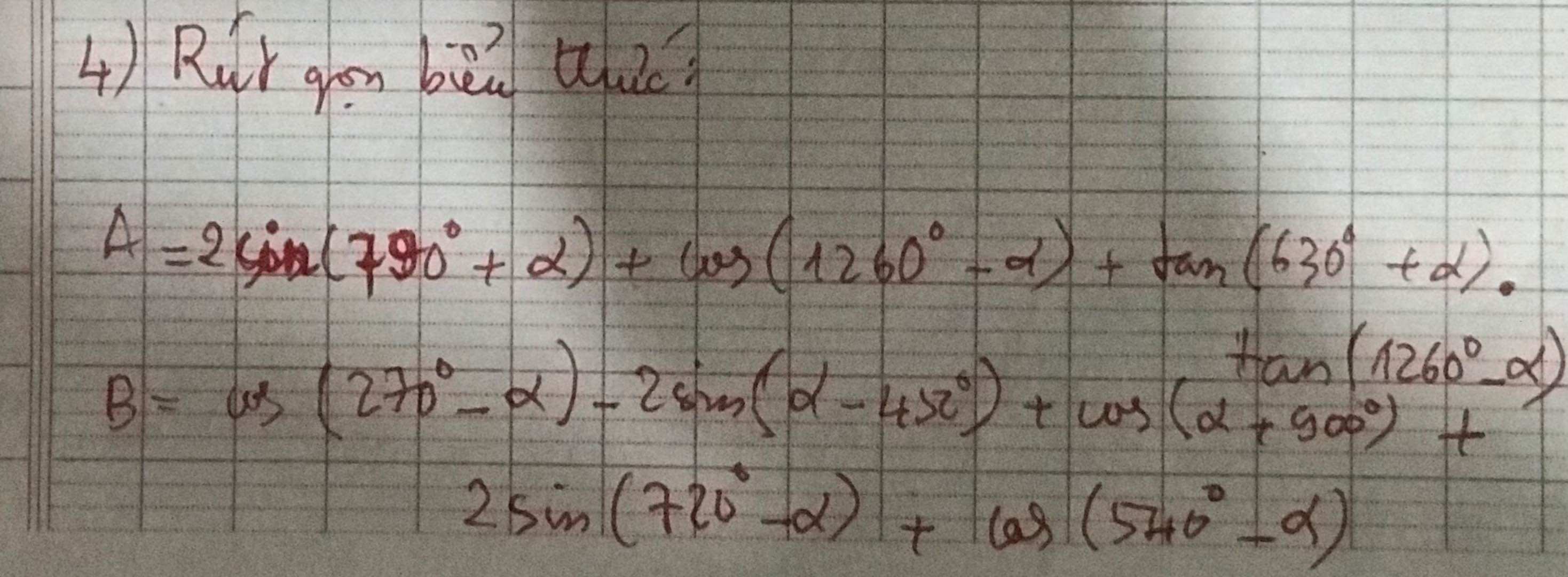\(B=cos\left(270^0-\alpha\right)-2\cdot\sin\left(\alpha-450^0\right)+cos\left(\alpha+90^0\right)+2\cdot\sin\left(720^0-\alpha\right)+cos\left(540^0-\alpha\right)\)
\(=cos\left(360^0-90^0-\alpha\right)-2\cdot\sin\left(\alpha-90^0-360^0\right)+cos\left(\alpha+90^0\right)+2\cdot\sin\left(-\alpha\right)+cos\left(180^0-\alpha\right)\)
\(=cos\left(-90^0-\alpha\right)-2\cdot\sin\left(\alpha-90^0\right)+cos\left(\alpha+90^0\right)-2\cdot\sin\alpha-cos\alpha\)
\(=cos\left(90^0+\alpha\right)+2\cdot\sin\left(90^0-\alpha\right)+cos\left(\alpha+90^0\right)-2\cdot\sin\alpha-cos\alpha\)
\(=2\cdot cos\left(90^0+\alpha\right)+2\cdot cos\alpha-2\cdot\sin\alpha-cos\alpha\)
\(=2\cdot\left(-\sin\alpha\right)-2\cdot\sin\alpha+cos\alpha=-4\cdot\sin\alpha+cos\alpha\)