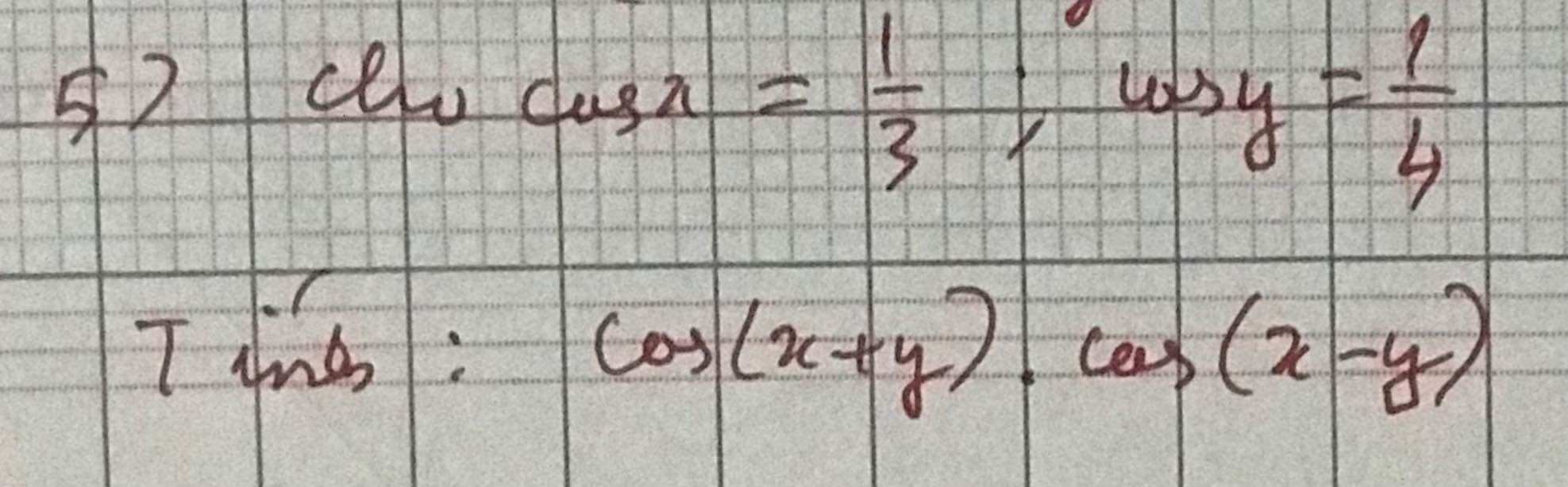\(cos\left(x+y\right)\cdot cos\left(x-y\right)\)
\(=\dfrac{1}{2}\cdot\left[cos\left(x+y+x-y\right)\cdot cos\left(x+y-x+y\right)\right]\)
\(=\dfrac{1}{2}\left[cos\left(2x\right)\cdot cos\left(2y\right)\right]\)
\(=\dfrac{1}{2}\left[\left(2cos^2x-1\right)\cdot\left(2\cdot cos^2y-1\right)\right]\)
\(=\dfrac{1}{2}\left[\left(2\cdot\dfrac{1}{9}-1\right)\cdot\left(2\cdot\dfrac{1}{16}-1\right)\right]\)
\(=\dfrac{1}{2}\left(\dfrac{2}{9}-1\right)\left(\dfrac{1}{8}-1\right)=\dfrac{1}{2}\cdot\dfrac{-7}{9}\cdot\dfrac{-7}{8}=\dfrac{49}{144}\)