d. Khúc này mình rút gọn B ở câu c nhé.
\(B=\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}\) (ĐK đã cho)
\(=\dfrac{x+2+\sqrt{x}\left(\sqrt{x}-1\right)-1\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}=\dfrac{\sqrt{x}-1}{x+\sqrt{x}+1}\)
Ta có : \(M=A.B\)
\(=\dfrac{2}{\sqrt{x}-1}\cdot\dfrac{\sqrt{x}-1}{x+\sqrt{x}+1}\)
\(=\dfrac{2\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}=\dfrac{2}{x+\sqrt{x}+1}\)
Xét \(x+\sqrt{x}+1\)
\(=x+2.\sqrt{x}\cdot\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)
\(=\left(\sqrt{x}+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)
Mà \(\left(\sqrt{x}+\dfrac{1}{2}\right)^2\ge0\) với mọi x không âm.
\(\Rightarrow\left(\sqrt{x}+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}>0\)
Lại có : \(M=\dfrac{2}{x+\sqrt{x}+1}=\dfrac{2}{\left(\sqrt{x}+\dfrac{1}{2}\right)^2+\dfrac{3}{4}}\) có 2 > 0.
Vậy : \(M=A.B>0\) (đpcm).






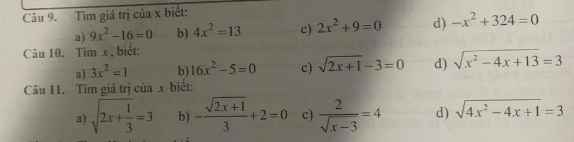











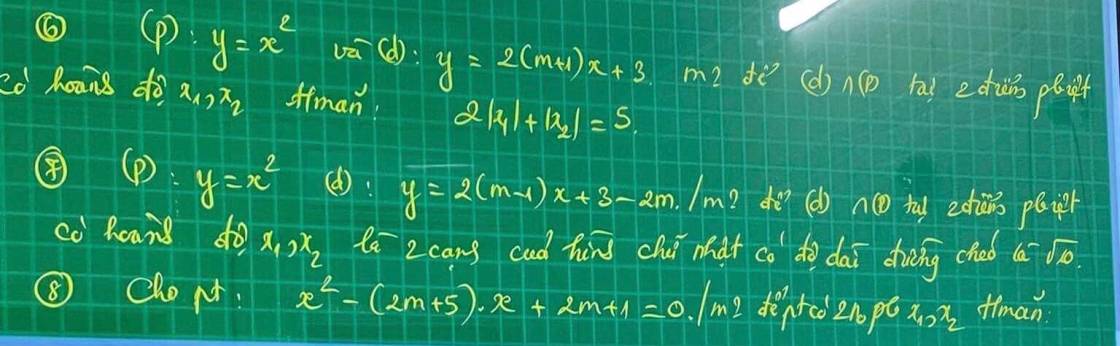

 Mọi người giúp mình câu 3, câu 4 với. Mình cảm ơn ạ. Mình đang cần gấp lắm!!!
Mọi người giúp mình câu 3, câu 4 với. Mình cảm ơn ạ. Mình đang cần gấp lắm!!!

