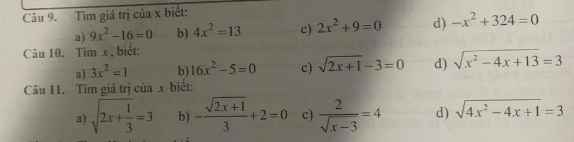Lời giải:
Đặt $\sqrt{x}=a(a\geq 0)$ thì pt trở thành:
$a^4+2a^3-5a^2-4a+6=0$
$\Leftrightarrow (a^4+2a^3+a^2)-6a^2-4a+6=0$
$\Leftrightarrow (a^2+a)^2-4(a^2+a)-2a^2+6=0$
$\Leftrightarrow (a^2+a)^2-4(a^2+a)+4-2(a^2-1)=0$
$\Leftrightarrow (a^2+a-2)^2-2(a^2-1)=0$
$\Leftrightarrow (a+2)^2(a-1)^2-2(a-1)(a+1)=0$
$\Leftrightarrow (a-1)[(a+2)^2(a-1)-2(a+1)]=0$
$\Leftrightarrow (a-1)(a^3+3a^2-2a-6)=0$
$\Leftrightarrow (a-1)[a^2(a+3)-2(a+3)]=0$
$\Leftrightarrow (a-1)(a+3)(a^2-2)=0$
$\Rightarrow a=1$ hoặc $a=\sqrt{2}$ (do $a\geq 0$)
$\Leftrightarrow x=1$ hoặc $x=2$
Lời giải:
Đặt $\sqrt{x}=a(a\geq 0)$ thì pt trở thành:
$a^4+2a^3-5a^2-4a+6=0$
$\Leftrightarrow (a^4+2a^3+a^2)-6a^2-4a+6=0$
$\Leftrightarrow (a^2+a)^2-4(a^2+a)-2a^2+6=0$
$\Leftrightarrow (a^2+a)^2-4(a^2+a)+4-2(a^2-1)=0$
$\Leftrightarrow (a^2+a-2)^2-2(a^2-1)=0$
$\Leftrightarrow (a+2)^2(a-1)^2-2(a-1)(a+1)=0$
$\Leftrightarrow (a-1)[(a+2)^2(a-1)-2(a+1)]=0$
$\Leftrightarrow (a-1)(a^3+3a^2-2a-6)=0$
$\Leftrightarrow (a-1)[a^2(a+3)-2(a+3)]=0$
$\Leftrightarrow (a-1)(a+3)(a^2-2)=0$
$\Rightarrow a=1$ hoặc $a=\sqrt{2}$ (do $a\geq 0$)
$\Leftrightarrow x=1$ hoặc $x=2$











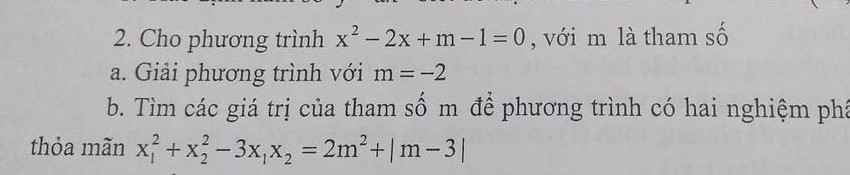



 Mọi người giúp mình câu 3, câu 4 với. Mình cảm ơn ạ. Mình đang cần gấp lắm!!!
Mọi người giúp mình câu 3, câu 4 với. Mình cảm ơn ạ. Mình đang cần gấp lắm!!!