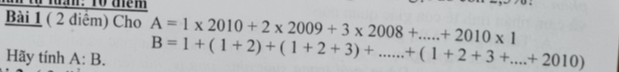\(A=1\cdot2010+2\cdot2009+3\cdot2008+...+2010\cdot1\)
\(=1\left(2011-1\right)+2\left(2011-2\right)+3\left(2011-3\right)+...+2010\left(2011-2010\right)\)
\(=2011\left(1+2+3+...+2010\right)-\left(1^2+2^2+3^2+...+2010^2\right)\)
\(=2011\cdot\dfrac{2010\cdot2011}{2}-\dfrac{2010\left(2010+1\right)\left(2\cdot2010+1\right)}{6}\)
\(=2011\cdot2011\cdot1005-335\cdot2011\cdot4021\)
\(=2011\cdot335\left(2011\cdot3-4021\right)\)
\(=2011\cdot335\cdot2012\)
\(B=1+\left(1+2\right)+\left(1+2+3\right)+...+\left(1+2+3+...+2010\right)\)
\(=1+\dfrac{2\cdot3}{2}+\dfrac{3\cdot4}{2}+...+\dfrac{2010\cdot2011}{2}\)
\(=\dfrac{1\cdot2+2\cdot3+...+2010\cdot2011}{2}\)
\(=\dfrac{1\left(1+1\right)+2\left(2+1\right)+...+2010\left(2010+1\right)}{2}\)
\(=\dfrac{\left(1^2+2^2+...+2010^2\right)+\left(1+2+...+2010\right)}{2}\)
\(=\dfrac{\dfrac{2010\left(2010+1\right)\left(2010\cdot2+1\right)}{6}+\dfrac{2010\cdot2011}{2}}{2}\)
\(=\dfrac{335\cdot2011\cdot4021+1005\cdot2011}{2}\)
\(=\dfrac{335\cdot2011\left(4021+3\right)}{2}\)
\(=335\cdot2011\cdot2012\)
=>A/B=1