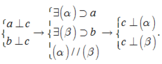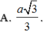Mệnh đề nào sau đây đúng?
A. Hai mặt phẳng vuông góc với nhau thì đường thẳng nào nằm trong mặt này cũng vuông góc với mặt kia
B. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau.
C. Một đường thẳng vuông góc với một trong hai mặt phẳng song song thì vuông góc với mặt phẳng kia.
D. Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì song song với nhau.
Đáp án C.
* Phương án A: Hai mặt phẳng vuông góc với nhau thì đường thẳng nào nằm trong mặt phẳng này mà vương góc với giao tuyến cũng vuông góc với mặt phẳng kia. Cụ thể: α ⊥ β α ∩ β = Δ d ∈ α : d ⊥ Δ → d ⊥ β .
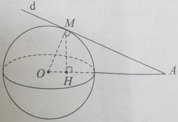
* Phương án B: Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba, hoặc hai mặt phẳng đó song song với nhau. Cụ thể: α ⊥ γ β ⊥ γ Δ = α ∩ β → Δ ⊥ γ α / / β
* Phương án C: Một đường thẳng vuông góc với một trong hai mặt phẳng song song thì vuông góc với mặt phẳng kia. Cụ thể α / / β Δ ⊥ α → Δ ⊥ β .
* Phương án D: Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì tồn tại hai mặt phẳng chứa hai đường thẳng đó và song song với nhau (hai mặt phẳng này cùng vuông góc với đường thẳng thứ 3).
Cụ thể: