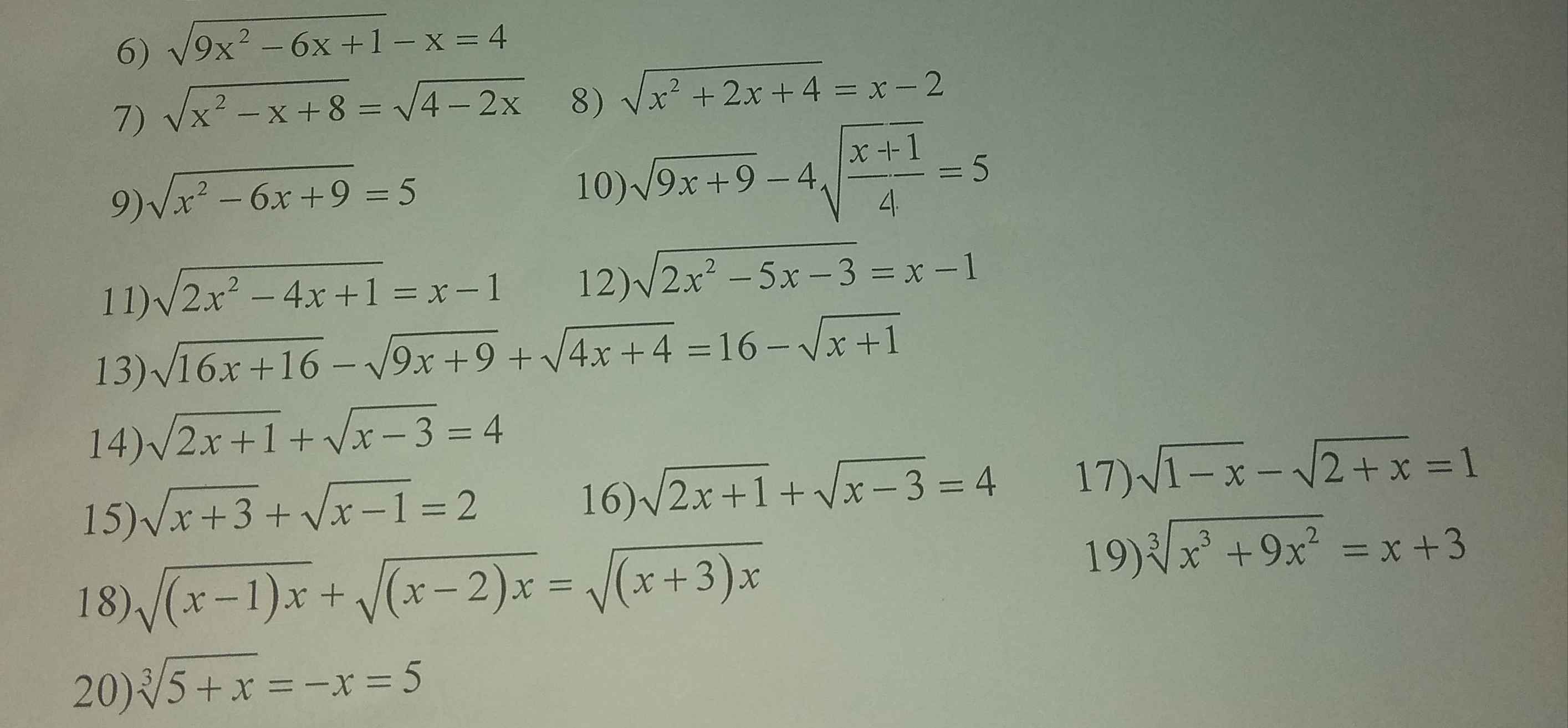19) Ta có: \(\sqrt[3]{x^3+9x^2}=x+3\)
\(\Leftrightarrow x^3+9x^2=\left(x+3\right)^3\)
\(\Leftrightarrow x^3+9x^2=x^3+9x^2+27x+27\)
\(\Leftrightarrow27x+27=0\)
\(\Leftrightarrow27x=-27\)
hay x=-1
Vậy: S={-1}
6) Ta có: \(\sqrt{9x^2-6x+1}-x=4\)
\(\Leftrightarrow\sqrt{\left(3x-1\right)^2}=x+4\)
\(\Leftrightarrow\left|3x-1\right|=x+4\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=x+4\left(x\ge\dfrac{1}{3}\right)\\1-3x=x+4\left(x< \dfrac{1}{3}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-x=4+1\\-3x-x=4-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=5\\-4x=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\left(nhận\right)\\x=\dfrac{-3}{4}\left(nhận\right)\end{matrix}\right.\)
Vậy: \(S=\left\{\dfrac{5}{2};\dfrac{-3}{4}\right\}\)
8)
ĐKXĐ: \(x>2\)
Ta có: \(\sqrt{x^2+2x+4}=x-2\)
\(\Leftrightarrow x^2+2x+4=\left(x-2\right)^2\)
\(\Leftrightarrow x^2+2x+4-x^2+4x-4=0\)
\(\Leftrightarrow6x=0\)
hay x=0(loại)
Vậy: \(S=\varnothing\)
9) Ta có: \(\sqrt{x^2-6x+9}=5\)
\(\Leftrightarrow\sqrt{\left(x-3\right)^2}=5\)
\(\Leftrightarrow\left|x-3\right|=5\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=5\\x-3=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-2\end{matrix}\right.\)
Vậy: S={8;-2}