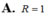Các câu hỏi tương tự
Cho
A
1
;
1
;
0
;
B
-
1
;
1
;
0
;
C
1
;
-
1
;
0
;
D...
Đọc tiếp
Cho A 1 ; 1 ; 0 ; B - 1 ; 1 ; 0 ; C 1 ; - 1 ; 0 ; D - 1 ; - 1 ; 0 là tâm của 4 mặt cầu có bán kính bằng 1. Gọi I là tâm mặt cầu (S) có bán kính bằng 1 tiếp xúc ngoài với cả 4 mặt cầu kể trên. Tính bán kính R của mặt cầu ngoại tiếp hình chóp I.ABCD.
![]()
![]()
![]()
![]()
Tìm bán kính R của mặt cầu (S) tâm
I
-
1
;
2
;
4
biết (S) cắt mặt phẳng (Oxy) theo giao tuyến là đường tròn (C) có bán kính
r
2
.
Đọc tiếp
Tìm bán kính R của mặt cầu (S) tâm I - 1 ; 2 ; 4 biết (S) cắt mặt phẳng (Oxy) theo giao tuyến là đường tròn (C) có bán kính r = 2 .
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I nằm trên tia Ox bán kính bằng 3 và tiếp xúc với mặt phẳng (Oyz). Viết phương trình mặt cầu (S).
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I nằm trên tia Ox bán kính bằng 3 và tiếp xúc với mặt phẳng (Oyz). Viết phương trình mặt cầu (S).
![]()
![]()
![]()
![]()
Trong Oxyz xét các mặt cầu bán kính bằng 1 và đều tiếp xúc với cả 3 mặt phẳng tọa độ. Gọi (S) là mặt cầu tiếp xúc trong với tất cả các mặt cầu trên. Tính bán kính R của (S).
Đọc tiếp
Trong Oxyz xét các mặt cầu bán kính bằng 1 và đều tiếp xúc với cả 3 mặt phẳng tọa độ. Gọi (S) là mặt cầu tiếp xúc trong với tất cả các mặt cầu trên. Tính bán kính R của (S).
![]()
![]()
![]()
![]()
Trong không gian Oxyz, tìm bán kính R của mặt cầu tâm I, tiếp xúc với mặt phẳng Oyz
A. R = 1
B. R = 2
C. R = 3
D. R = 13
Cho I(4;-4;1). Viết phương trình mặt cầu (S) tâm I sao cho (S) cắt mặt phẳng (Oxy) theo một đường tròn có bán kính
r
2
.
Đọc tiếp
Cho I(4;-4;1). Viết phương trình mặt cầu (S) tâm I sao cho (S) cắt mặt phẳng (Oxy) theo một đường tròn có bán kính r = 2 .
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho ba điểm A(10;1;1), B(10;4;1) và C(10;1;5). Gọi
S
1
là mặt cầu có tâm A, bán kính bằng 1; gọi
S
2
là mặt cầu có tâm B, bán kính bằng 2 và
S
3
là mặt cầu có tâm C, bán kính bằng 4. Hỏi có bao nhiêu mặt phẳng tiếp xúc với cả ba mặt cầu. A.4. B.7. C.2. D. 3.
Đọc tiếp
Trong không gian Oxyz, cho ba điểm A(10;1;1), B(10;4;1) và C(10;1;5). Gọi S 1 là mặt cầu có tâm A, bán kính bằng 1; gọi S 2 là mặt cầu có tâm B, bán kính bằng 2 và S 3 là mặt cầu có tâm C, bán kính bằng 4. Hỏi có bao nhiêu mặt phẳng tiếp xúc với cả ba mặt cầu.
A.4.
B.7.
C.2.
D. 3.
Trong không gian Oxyz, mặt cầu tâm I(1;1;-2) tiếp xúc với mặt phẳng (P): x + 2y - 2z + 5 = 0 có bán kính bằng
A. 2
B. 4
C. 3
D. 6
Xét tám mặt cầu có bán kính bằng 1 và các mặt cầu này đều tiếp xúc với cả ba mặt phẳng tọa độ. Tìm bán kính mặt cầu (S) mà cả tám mặt cầu kể trên đều tiếp xúc trong với (S)
Đọc tiếp
Xét tám mặt cầu có bán kính bằng 1 và các mặt cầu này đều tiếp xúc với cả ba mặt phẳng tọa độ. Tìm bán kính mặt cầu (S) mà cả tám mặt cầu kể trên đều tiếp xúc trong với (S)
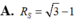
![]()
![]()
![]()