Các câu hỏi tương tự
Rút gọn biểu thức M=(x^3+y^3+z^3-3xyz)/ x^2+y^2+z^2-xy-yz-zx
Cho x,y,z,t >0
C/m : \(\left(x+y+z+t\right)\left(\frac{1}{x+y+z}+\frac{1}{y+z+t}+\frac{1}{z+t+x}+\frac{1}{t+x+y}\right)\ge\frac{16}{3}\)
1.a.rút gọn biểu thức M = \(\dfrac{\text{1}}{\text{(x - y)(z² + yz - x² - xy)}}-\dfrac{\text{1}}{\text{(y - z)(x² + xz - y² -yz)}}+\dfrac{\text{1}}{\text{(z - x)(y² + xy - z² - xz)}}\)
b. tính giá trị của M tại x = y = z = 2015
giải hệ pt x+y+z+1/x+1/y+1/z=51/4 và x^2+y^2+z^2+1/x^2+1/y^2+1/z^2=771/16
Rút gọn biểu thức :
\(\frac{\left[\left(e-m\right)^2-\left(e+m\right)^2\right].\left[\left(y-1\right)^2-\left(y+1\right)^2\right]}{a.16.n.h}.\frac{ê}{u^{-1}}\)
x + 3 y +z 3 -2x - y + z -2 x + 4y + 2z m Tìm m để hệ pt trên có nghiệm duy nhất (z;y;z) sao cho x2 +y2+z2 đạt giá trị nhỏ nhất?
Đọc tiếp
Tìm m để hệ pt trên có nghiệm duy nhất (z;y;z) sao cho x2 +y2+z2 đạt giá trị nhỏ nhất?
a) Tìm ĐKXĐ và rút gọn M
b) Tìm x thuộc Z để M thuộc Z. Tìm giá trị nguyên đó
c) Tìm x thỏa mãn M<0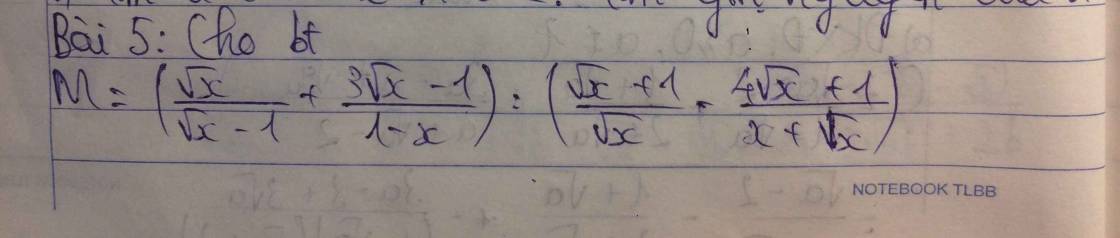
Cho \(M=\frac{a+\sqrt{a}-2}{a-\sqrt{a}+2}\)
a. Rút gọn M
b. Tìm a thuộc Z dể M thuộc Z
c. Tìm a thuộc Q dể M thuộc Z
1,cmr frac{2sqrt{mn}}{sqrt{n}+sqrt{n}+sqrt{m+n}}sqrt{m}+sqrt{n}-sqrt{m+n}1,rút gọn a, 3sqrt{27a}+2sqrt{frac{a}{3}}+asqrt{frac{4}{3a}}b,x^2sqrt{frac{12y}{x}}-xysqrt{frac{x}{3y}}c,frac{x}{left(sqrt{x}-sqrt{y}right)left(sqrt{x}-sqrt{z}right)}+frac{y}{left(sqrt{y}-sqrt{z}right)left(sqrt{y}-sqrt{x}right)}+frac{z}{left(sqrt{z}-sqrt{x}right)left(sqrt{z}-sqrt{y}right)}
Đọc tiếp
1,cmr
\(\frac{2\sqrt{mn}}{\sqrt{n}+\sqrt{n}+\sqrt{m+n}}\)=\(\sqrt{m}+\sqrt{n}-\sqrt{m+n}\)
1,rút gọn
a, 3\(\sqrt{27a}+2\sqrt{\frac{a}{3}}+a\sqrt{\frac{4}{3a}}\)
b,\(x^2\sqrt{\frac{12y}{x}}-xy\sqrt{\frac{x}{3y}}\)
c,\(\frac{x}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}-\sqrt{z}\right)}+\frac{y}{\left(\sqrt{y}-\sqrt{z}\right)\left(\sqrt{y}-\sqrt{x}\right)}+\frac{z}{\left(\sqrt{z}-\sqrt{x}\right)\left(\sqrt{z}-\sqrt{y}\right)}\)
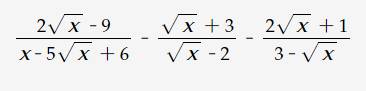
Rút gọn và tìm x thuộc z để M nguyên











