Các câu hỏi tương tự
Thời gian và vận tốc của một vật khi nó đang trược xuống mặt phẳng nghiêng được xác định bởi công thức
∫
2
20
-
3
v
d
v
(giây). Chọn gốc thời gian là lúc vật bắt đầu chuyển động. Hãy tìm phương trình vận tốc A.
20
3
-
20
3
-...
Đọc tiếp
Thời gian và vận tốc của một vật khi nó đang trược xuống mặt phẳng nghiêng được xác định bởi công thức ∫ 2 20 - 3 v d v (giây). Chọn gốc thời gian là lúc vật bắt đầu chuyển động. Hãy tìm phương trình vận tốc
A. 20 3 - 20 3 - 3 t 2
B. 20 3 + 20 3 - 3 t 2
C. 20 3 - 20 3 - 3 t 2 hoặc 20 3 + 20 3 - 3 t 2
D. 4 + 4 e - 3 t 2
Trong không gian (Oxyz), cho vật thể (H) giới hạn bởi hai mặt phẳng có phương trình x a và x b (
b
a
) Gọi S(x) là diện tích thiết diện của (H) bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x, với
a
≤
x
≤
b
.
Giả sử hàm số
y
S
(
x
)
liên tục trên đoạn [a;b]. Khi đó, thể tích V của vật thể (H) được cho b...
Đọc tiếp
Trong không gian (Oxyz), cho vật thể (H) giới hạn bởi hai mặt phẳng có phương trình x = a và x = b ( b < a ) Gọi S(x) là diện tích thiết diện của (H) bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x, với a ≤ x ≤ b . Giả sử hàm số y = S ( x ) liên tục trên đoạn [a;b]. Khi đó, thể tích V của vật thể (H) được cho bởi công thức:
A. V = π ∫ a b S ( x ) 2 d x
B. V = π ∫ a b S ( x ) d x
C. V = ∫ a b S ( x ) 2 d x
D. V = ∫ a b S ( x ) d x
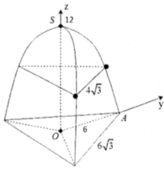
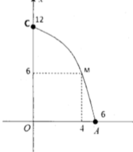
Cho một vật thể có dạng như hình vẽ. Ba cạnh là ba đường parabol giống nhau, mọi mặt phẳng vuông góc với đường cao SO của vật thể đều cắt nó theo thiết diện là tam giác đều. Mặt phẳng trung trực của đường cao cắt vật thể theo thiết diện là tam giác đều có cạnh bằng 4
3
m
Đáy là tam giác đều có cạnh bằng 6
3
m
Đọc tiếp
Cho một vật thể có dạng như hình vẽ. Ba cạnh là ba đường parabol giống nhau, mọi mặt phẳng vuông góc với đường cao SO của vật thể đều cắt nó theo thiết diện là tam giác đều. Mặt phẳng trung trực của đường cao cắt vật thể theo thiết diện là tam giác đều có cạnh bằng 4
3
m
Đáy là tam giác đều có cạnh bằng 6
3
m
![]()
![]()
![]()
![]()
Một vật thể nằm giữa hai mặt phẳng x-1; x1 và thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ
x
(
-
1
≤
x
≤
1
)
là một hình tròn có diện tích bằng
3
π
. Thể tích của vật thể là A. 3
π
2
B. 6
π
C. 6. D. 2
π
Đọc tiếp
Một vật thể nằm giữa hai mặt phẳng x=-1; x=1 và thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ x ( - 1 ≤ x ≤ 1 ) là một hình tròn có diện tích bằng 3 π . Thể tích của vật thể là
A. 3 π 2
B. 6 π
C. 6.
D. 2 π
Một vật thể nằm giữa hai mặt phẳng
x
-
1
,
x
1
và thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ
x
-
1
≤
x
≤
1
là một hình tròn có diện tích bằng 3π. Thể tích của vật thể là A.
3
π
2
B....
Đọc tiếp
Một vật thể nằm giữa hai mặt phẳng x = - 1 , x = 1 và thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ x - 1 ≤ x ≤ 1 là một hình tròn có diện tích bằng 3π. Thể tích của vật thể là
A. 3 π 2
B. 6 π
C. 6
D. 2 π
Tính thể tích vật thể bị giới hạn bởi các mặt phẳng x 0 và x 1, biết thiết diện của vật thể khi cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ
x
0
≤
x
≤
1
là một hình vuông có độ dài cạnh
x
e
x
-
1
. A....
Đọc tiếp
Tính thể tích vật thể bị giới hạn bởi các mặt phẳng x = 0 và x =1, biết thiết diện của vật thể khi cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x 0 ≤ x ≤ 1 là một hình vuông có độ dài cạnh x e x - 1 .
A. V = π 2
B. V = e - 1 2
C. V = 1 2
D. V = π e - 1 2
Các lực tác dụng lên một vật gọi là cân bằng khi
A. hợp lực của tất cả các lực tác dụng lên vật bằng không.
B. hợp lực của tất cả các lực tác dụng lên vật là hằng số.
C. vật chuyển động với gia tốc không đổi.
D. vật đứng yên.
Cắt một vật thể (T) bởi hai mặt phẳng (P) và (Q) vuống góc với trục Ox lần lượt tại . Một mặt phẳng tùy ý vuông góc với trục Ox tại điểm x
a
≤
x
≤
b
cắt (T) theo thiết diện có diện tích là S(x) liên tục trên đoạn [a; b]. Thể tích V của phần vật thể (T) giới hạn bởi hai mặt phẳng (P) và (Q) được cho bởi công thức nào dưới đây? A.
V
π...
Đọc tiếp
Cắt một vật thể (T) bởi hai mặt phẳng (P) và (Q) vuống góc với trục Ox lần lượt tại . Một mặt phẳng tùy ý vuông góc với trục Ox tại điểm x a ≤ x ≤ b cắt (T) theo thiết diện có diện tích là S(x) liên tục trên đoạn [a; b]. Thể tích V của phần vật thể (T) giới hạn bởi hai mặt phẳng (P) và (Q) được cho bởi công thức nào dưới đây?
A. V = π ∫ a b S 2 x dx
B. V = ∫ a b S x dx
C. V = π ∫ a b S x dx
D. V = π 2 ∫ a b S x dx
Cắt một vật thể
T
bởi hai mặt phẳng
P
và
Q
vuông góc với trục Ox lần lượt tại
x
a
,
x
b
a
b
. Một mặt phẳng tùy ý vuông góc với trục Ox tại điểm
x
a
≤
x
≤
b...
Đọc tiếp
Cắt một vật thể T bởi hai mặt phẳng P và Q vuông góc với trục Ox lần lượt tại x = a , x = b a < b . Một mặt phẳng tùy ý vuông góc với trục Ox tại điểm x a ≤ x ≤ b cắt T theo thiết diện có diện tích là S x . Giả sử S x liên tục trên đoạn a ; b . Thể tích V của phần vật thể giới hạn bởi hai mặt phẳng P và Q được cho bởi công thức nào dưới đây?
A. V = π ∫ a b S 2 x dx
B. V = ∫ a b S x dx
C. V = π ∫ a b S x dx
D. V = π 2 ∫ a b S x dx



