Đáp án B.
Ta có lim x → + ∞ x − 2 x + 3 = lim x → + ∞ 1 − 2 x 1 + 3 x = 1.
Đáp án B.
Ta có lim x → + ∞ x − 2 x + 3 = lim x → + ∞ 1 − 2 x 1 + 3 x = 1.
Cho hàm số y = f x = a x 3 + b x 3 + c x + d a , b , c , d ∈ ℝ ; a ≠ 0 biết f'(-1)=3. Tính lim ∆ x → ∞ f 1 + ∆ x + f 1 ∆ x
A. 3
B. -3
C. 1
D. -1
Cho hàm số f x = a x + b cx + d với a,b,c,d là các số thực và c ≠ 0 Biết f 1 = 1 , f 2 = 2 và f f x = x với mọi x ≠ - d c Tính lim x → ∞ f x
A. 3 2
B. 5 6
C. 2 3
D. 6 5
tìm x thuộc Z,biết
a)(x2+2)(x+3)>0
b)(x-2)(-4-x2)>0
c)(x+4)|x+5|lớn hơn hoặc bằng 0
d)(x+3)(x-4)<0
Giới hạn lim x → 3 x + 1 - 5 x + 1 x - 4 x - 3 bằng a b (phân số tối giản). Giá trị của a - b là:
A. 1
B. 1 9
C. -1
D. 2
Cho 2 đa thức
A(x)= -x^2-3+5x^4-1/3x^3+1
B(x)= -3/4x^3+2-x^2+4x
a) Sắp xếp theo lũy thừa giảm dần của biến
b) Tính A(x)+B(x)
c) x=1 là nghiệm của đa thức A(x)+B(x)? Vì sao?
bài 3: tính nhanh:
a) -5 phần 9 + 3 phần 5 - 3 phần 9 + -2 phần 5
b) 5 phần 17 - 9 phần 15 - 2 phần 17 + -2 phần 5
c) ( 1 phần 9 - 9 phần 17 ) + 3 phần 6 - ( 12 phần 17 - 1 phần 2 ) + 5 phần 9
bài 4: tìm x
a) 3 phần 4 - x = 1
b) x + 4 = 1 phần 5
c) x phần 4 - 3 phần 7 + 2 phần 5 = 31 phần 140
Toán 6 ! giúp mình đi mình tick cho các bạn!
d) 5 phần 12 + 5 phần x - 1 phần 8 = 1 phần 2
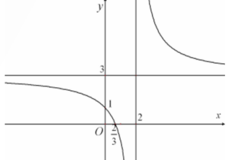
Cho các phát biểu sau (1): Hàm số y = x 3 + 3 x 2 + 3 x + 1 có đồ thị là (C) không có cực trị (2).Hàm số y = x 3 + 3 x 2 + 3 x + 1 có điểm uốn là U(-1;0) (3). Đồ thị hàm số y = 3 x - 2 x - 2 có dạng.Hàm số y = 2 x + 1 x + 1 có lim x → 1 + 2 x + 1 x + 1 = - ∞ và lim x → 1 - 2 x + 1 x + 1 = + ∞ .Số các phát biểu đúng là:
A. 1
B. 2
C. 3
D. 0
1. Cho hàm số y=2x-1/x-1 . Lấy M thuộc C với XM=m . tiếp tuyến của C tại M cắt 2 đường tiệm cận tại A,B . Gọi I là giao của 2 đường tiệm cận . CMR : M là trung điểm của AB và tam giác IAB có diện tích không phụ thuộc vào M
2.cho y=x+2/x-3 tìm M thuộc C sao cho khoảng cách từ M đến 2 đường tiệm cận C bằng nhau
3. cho y = x+2/x-2 tìm M thuộc C sao cho M cách đều hai trục tọa độ . viết pttt của C biết tiếp tuyến đó đi qua A(-6;5)
4 . cho y = x+1/x-1 . CMR (d) : 2x-y+m=0 luôn cắt C tại A,B trên 2 nhánh của (C) . tìm m để AB ngắn nhất
lim x → + ∞ x - 3 x + 2 bằng
A. - 3 2
B. 1
C. - 2
D. 3
Cho hàm số f x = a x + b c x + d với a , b , c , d ∈ R có đồ thị hàm số y=f'(x) như hình vẽ bên. Biết rằng giá trị lớn nhất của hàm số y=f(x) trên đoạn [-3;-2] bằng 8. Giá trị của f(2) bằng.

A. 2
B. 5
C. 4
D. 6