Các câu hỏi tương tự
Cho f(x)
log
5
(
sin
x
)
,
x
∈
(
0
;
π
/
2
)
. Tính f(x)
Đọc tiếp
Cho f(x)= log 5 ( sin x ) , x ∈ ( 0 ; π / 2 ) . Tính f'(x)
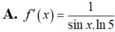
![]()
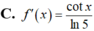
![]()
Biết F(x) là một nguyên hàm của hàm số
f
x
e
-
x
+
sin
x
thỏa mãn F(0) 0. Tìm F(x)?
Đọc tiếp
Biết F(x) là một nguyên hàm của hàm số f x = e - x + sin x thỏa mãn F(0) = 0. Tìm F(x)?
![]()
![]()
![]()
![]()
Xét sự đồng biến, nghịch biến của các hàm số:
a) y = x − sinx, x ∈ [0; 2π].
c) y = sin(1/x), (x > 0)
Đạo hàm của hàm số
y
sin
x
+
log
3
x
3
(x 0)
Đọc tiếp
Đạo hàm của hàm số y = sin x + log 3 x 3 (x > 0)
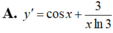
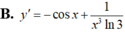
![]()
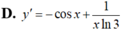
Xét sự đồng biến, nghịch biến của các hàm số: y = sin(1/x), (x > 0)
Giá trị lớn nhất của hàm số f(x) = sin x + cos 2x trên [0; π ] là
A. 5 4
B. 1
C. 2
D. 9 8
Biết F(x) là một nguyên hàm của hàm số f(x) = sin 2x + cosx. Giá trị F π 2 - F ( 0 ) bằng
A. 2.
B. 1.
C. -1.
D. 4.
1. Tìm m sao cho \(y=\frac{m\sin x+4}{\sin x+m}\)nghịch biến trên \(\left(0,\frac{\eta}{2}\right)\)
2. Tìm m sao cho \(y=\frac{\cos x+1}{m\cos x+2}\)nghịch biến trên \(\left(0,\frac{\eta}{2}\right)\)
Cho hàm số
f x = 1 3 x 3 - 1 2 x 2 - 4 x + 6
Giải phương trình f'(sin x) = 0.



