Bài 3:
1: Xét tứ giác AEHF có \(\hat{AEH}=\hat{AFH}=\hat{FAE}=90^0\)
nên AEHF là hình chữ nhật
2: ta có: BD⊥BA
AC⊥BA
Do đó: BD//AC
=>BD//CF
Xét ΔMDB và ΔMFC có
\(\hat{MBD}=\hat{MCF}\) (hai góc so le trong, BD//CF)
MB=MC
\(\hat{DMB}=\hat{FMC}\) (hai góc đối đỉnh)
Do đó: ΔMDB=ΔMFC
=>DB=FC
Xét tứ giác BDCF có
BD//CF
BD=CF
Do đó: BDCF là hình bình hành
3: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MC
=>ΔMAC cân tại M
=>\(\hat{MAC}=\hat{MCA}=\hat{ACB}\)
AEHF là hình chữ nhật
=>\(\hat{AFE}=\hat{AHE}\)
mà \(\hat{AHE}=\hat{ABC}\left(=90^0-\hat{HAE}\right)\)
nên \(\hat{AFE}=\hat{ABC}\)
\(\hat{AFE}+\hat{MAC}=\hat{ABC}+\hat{ACB}=90^0\)
=>AM⊥FE

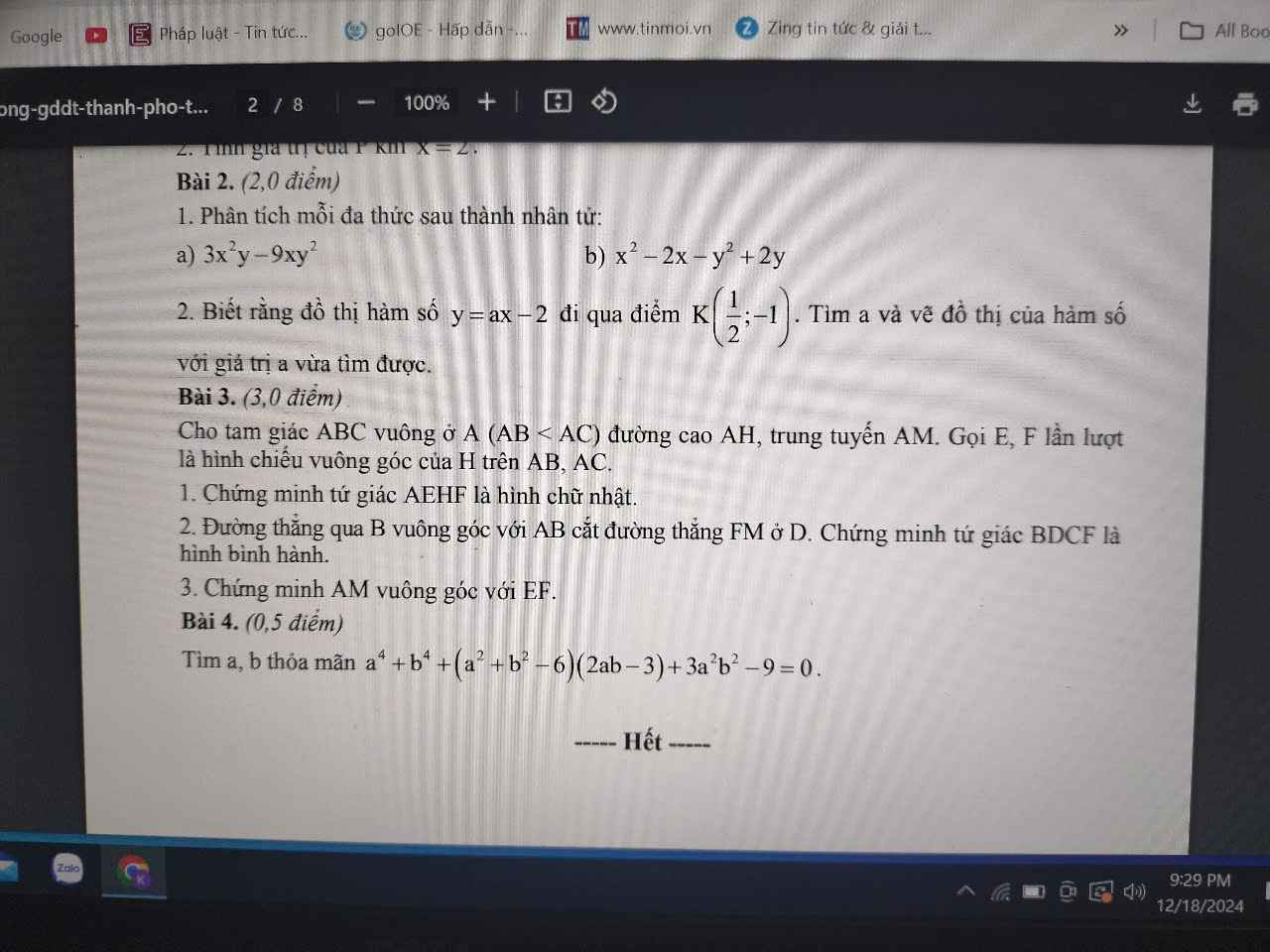








 Giúp e bài 2 thôi ạ bài 1 e làm r ạ! Mong mn giúp e, e cần gấp ạ!
Giúp e bài 2 thôi ạ bài 1 e làm r ạ! Mong mn giúp e, e cần gấp ạ!







 em cần giải gấp bài 3 chi tiết mọi người giúp em với ạ. Làm bài dưới dạng phân số ạ em cần gấp
em cần giải gấp bài 3 chi tiết mọi người giúp em với ạ. Làm bài dưới dạng phân số ạ em cần gấp