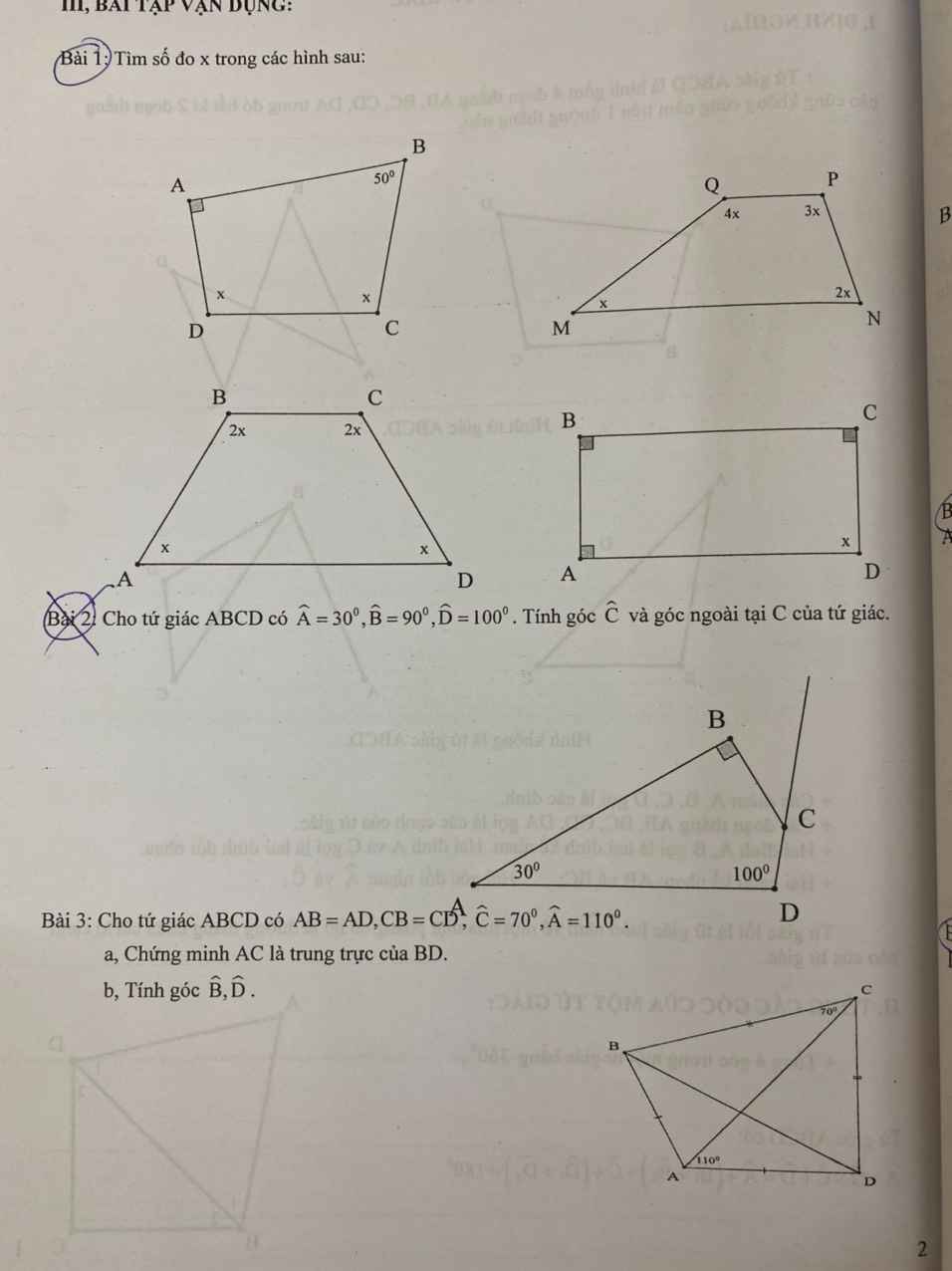
Tứ giác ABCD có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\) (tổng bốn góc trong một tứ giác)
\(90^0+50^0+x+x=360^0\)
\(140^0+2x=360^0\)
\(2x=360^0-140^0\)
\(2x=220^0\)
\(x=\dfrac{220^0}{2}\)
\(x=110^0\)
Tứ giác MNPQ có:
\(\widehat{M}+\widehat{N}+\widehat{P}+\widehat{Q}=360^0\) (tổng bốn góc trong một tứ giác)
\(x+2x+3x+4x=360^0\)
\(10x=360^0\)
\(x=\dfrac{360^0}{10}\)
\(x=36^0\)
Tứ giác ABCD có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\) (tổng bốn góc trong một tứ giác)
\(x+2x+2x+x=360^0\)
\(6x=360^0\)
\(x=\dfrac{360^0}{6}=60^0\)
Bài 1:
\(a,x+x+50^o+90^o=360^o.\\ \Rightarrow2x=360^o-50^o-90^o=220^o.\\ \Leftrightarrow x=110^o.\)
\(b,4x+3x+2x+x=360^o.\\ \Leftrightarrow10x=360^o.\\ \Leftrightarrow x=36^o.\)
\(c,2x+2x+x+x=360^o.\\ \Leftrightarrow6x=360^o.\\ \Leftrightarrow x=60^o.\)
\(d,90^o+90^o+90^o+x=360^o.\\ \Rightarrow x=360^o-90^o-90^o-90^o=90^o.\)
Bài 3:
Ta có:
\(\text{+) AB = AD (gt).}\)
\(\Rightarrow\) \(A\in\) đường trung trực của đoạn thẳng BD. (1)
\(\text{+) CB = CD (gt).}\)
\(\Rightarrow\) \(C\in\) đường trung trực của đoạn thẳng BD. (2)
Từ (1) và (2) ta suy ra AC là đường trung trực của đoạn thẳng BD.
Tứ giác ABCD có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\) (tổng bốn góc trong một tứ giác)
\(90^0+90^0+90^0+x=360^0\)
\(270^0+x=360^0\)
\(x=360^0-270^0=90^0\)