a: \(P=\dfrac{\sqrt{x}+1+\sqrt{x}}{x-1}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{2\sqrt{x}+1}=\dfrac{\sqrt{x}}{\sqrt{x}+1}\)
b: Để P<1/2 thì P-1/2<0
\(\Leftrightarrow\dfrac{\sqrt{x}}{\sqrt{x}+1}-\dfrac{1}{2}< 0\)
=>2 căn x-căn x-1<0
=>0<x<1
`a)` Với `x \ne 1,x >= 0` có:
`P=(1/[\sqrt{x}-1]+\sqrt{x}/[x-1]).[x-\sqrt{x}]/[2\sqrt{x}+1]`
`P=[\sqrt{x}+1+\sqrt{x}]/[(\sqrt{x}-1)(\sqrt{x}+1)].[\sqrt{x}(\sqrt{x}-1)]/[2\sqrt{x}+1]`
`P=\sqrt{x}/[\sqrt{x}+1]`
__________________________________________________
`b)` Với `x >= 0,x \ne 1` có:
`P < 1/2<=>\sqrt{x}/[\sqrt{x}+1]-1/2 < 0`
`<=>[2\sqrt{x}-\sqrt{x}-1]/[2(\sqrt{x}+1)] < 0`
Với `x >= 0<=>2(\sqrt{x}+1) > 0`
`=>\sqrt{x}-1 < 0`
`<=>\sqrt{x} < 1`
`<=>x < 1` Kết hợp đk
`=>0 <= x < 1`
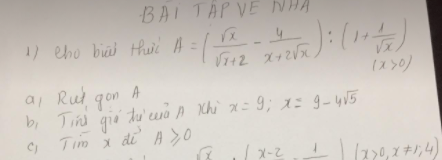
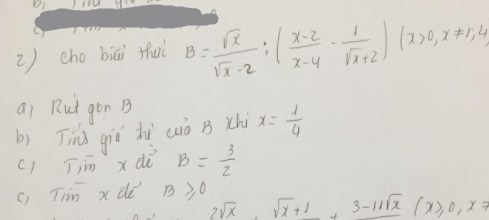
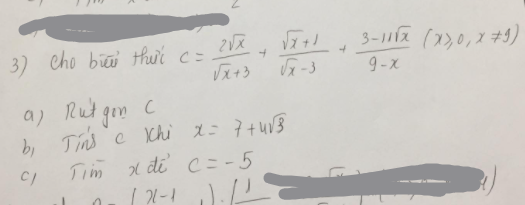
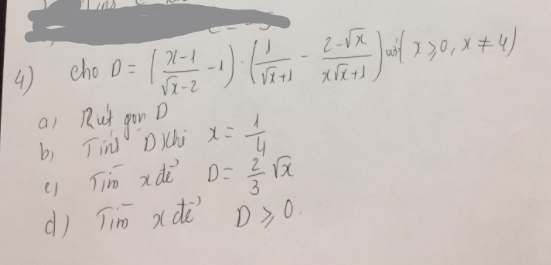
bạn nào có thể làm giúp mình bài này theo những ý như này được không ạ
