a: Thay m=-2 vào hệ, ta được:
\(\left\{{}\begin{matrix}3x-2y=5\\x+\left(-2+1\right)y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-2y=5\\x-y=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x-2y=5\\3x-3y=21\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-2y-3x+3y=5-21=-16\\x-y=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=-16\\x=y+7=-16+7=-9\end{matrix}\right.\)
b: Để hệ có nghiệm duy nhất thì \(\dfrac{3}{1}\ne\dfrac{-2}{m+1}\)
=>\(m+1\ne-\dfrac{2}{3}\)
=>\(m\ne-\dfrac{2}{3}-1=-\dfrac{5}{3}\)
\(\left\{{}\begin{matrix}3x-2y=5\\x+\left(m+1\right)y=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x-2y=5\\3x+\left(3m+3\right)y=21\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x+\left(3m+3\right)y-3x+2y=21-5\\3x-2y=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(3m+5\right)y=16\\3x=2y+5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{16}{3m+5}\\3x=2\cdot\dfrac{16}{3m+5}+5=\dfrac{32+15m+25}{3m+5}=\dfrac{15m+57}{3m+5}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{16}{3m+5}\\x=\dfrac{5m+19}{3m+5}\end{matrix}\right.\)
x=-3y
=>\(\dfrac{5m+19}{3m+5}=\dfrac{-3\cdot16}{3m+5}=\dfrac{-48}{3m+5}\)
=>5m+19=-48
=>5m=-48-19=-67
=>\(m=-\dfrac{67}{5}\left(nhận\right)\)
c: Để x,y nguyên thì \(\left\{{}\begin{matrix}16⋮3m+5\\5m+19⋮3m+5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}16⋮3m+5\\15m+57⋮3m+5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}16⋮3m+5\\15m+25+32⋮3m+5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}16⋮3m+5\\32⋮3m+5\end{matrix}\right.\Leftrightarrow16⋮3m+5\)
=>\(3m+5\in\left\{1;-1;2;-2;4;-4;8;-8;16;-16\right\}\)
=>\(m\in\left\{-\dfrac{4}{3};-2;-1;-\dfrac{7}{3};-\dfrac{1}{3};-3;1;-\dfrac{13}{3};\dfrac{11}{3};-7\right\}\)
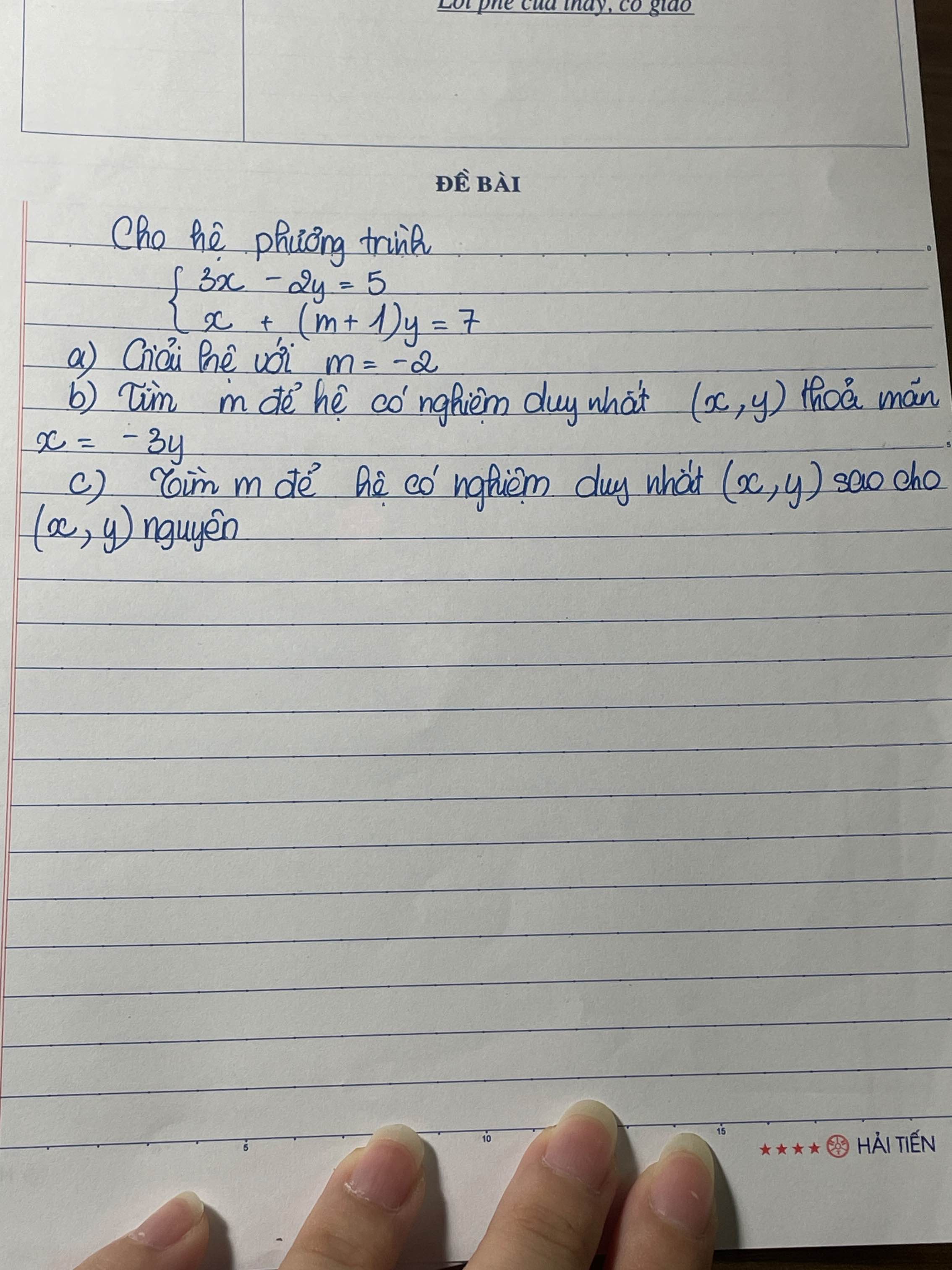
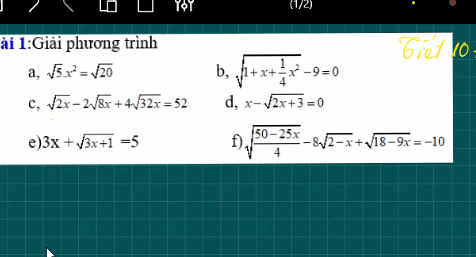
mọi người lập bảng giải hộ em bằng hệ phương trình với ạ. E cần gấp, em cảm ơn
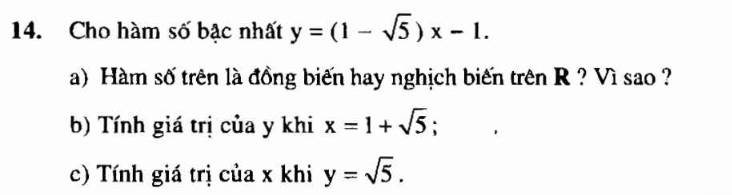giúp e với aa, e cảm ơn nhiềuu
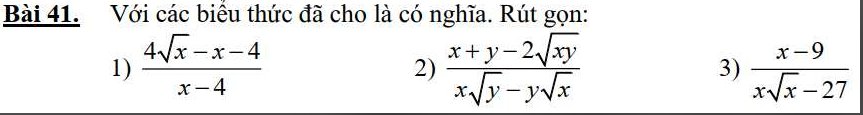giúp e gấp với ạ, e cảm ơn
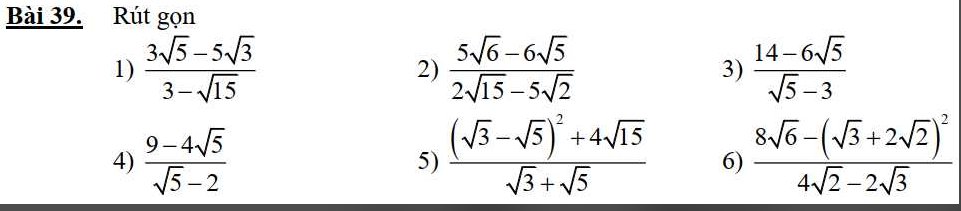làm rõ ra giúp e ạ, e cảm ơn