Bài 1:
a: \(A=\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\)
\(=\dfrac{x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}\)
\(=\dfrac{x+2+\sqrt{x}\left(\sqrt{x}-1\right)-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{-\sqrt{x}+1+x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}-1}{x+\sqrt{x}+1}\)
b:
\(\sqrt{A}\) được xác định khi A>=0
=>\(\dfrac{\sqrt{x}-1}{x+\sqrt{x}+1}>=0\)
=>\(\sqrt{x}-1>=0\)
=>x>=1
Kết hợp ĐKXĐ, ta được: x>1
\(A-1=\dfrac{\sqrt{x}-1}{x+\sqrt{x}+1}-1=\dfrac{\sqrt{x}-1-x-\sqrt{x}-2}{x+\sqrt{x}+1}\)
\(=\dfrac{-x-3}{x+\sqrt{x}+1}< 0\)
=>A<1
=>\(\sqrt{A}>A\)
=>\(A< \sqrt{A}\)
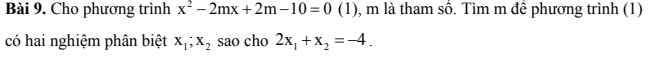
Mọi người giúp e làm câu 4c và bài 5 ạ
