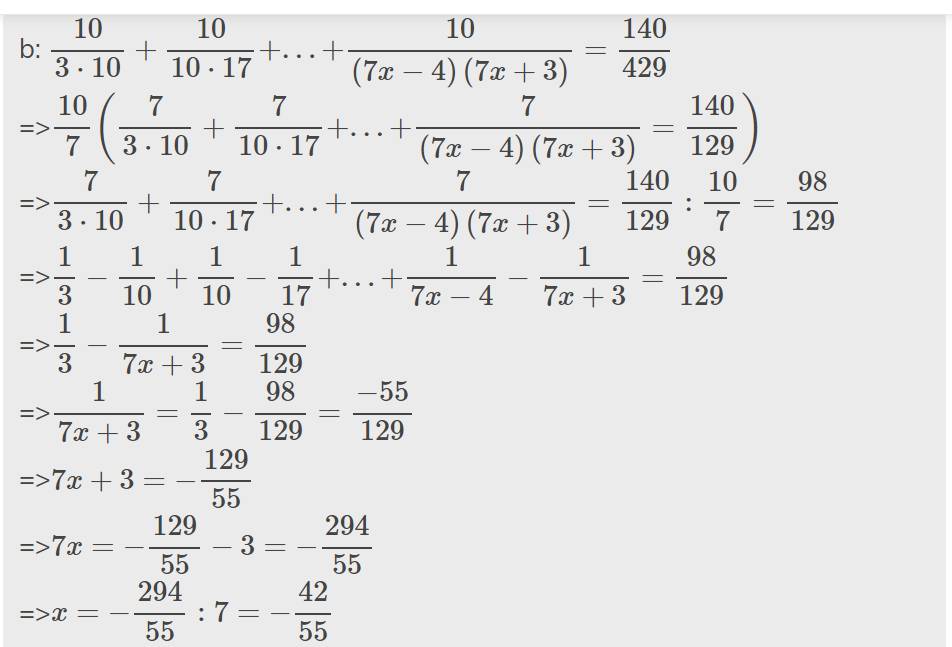d: \(\dfrac{1}{5\cdot105}+\dfrac{1}{6\cdot106}+...+\dfrac{1}{14\cdot114}\)
\(=\dfrac{1}{100}\left(\dfrac{100}{5\cdot105}+\dfrac{100}{6\cdot106}+...+\dfrac{100}{14\cdot114}\right)\)
\(=\dfrac{1}{100}\left(\dfrac{1}{5}-\dfrac{1}{105}+\dfrac{1}{6}-\dfrac{1}{106}+...+\dfrac{1}{14}-\dfrac{1}{114}\right)\)
\(\dfrac{1}{5\cdot15}+\dfrac{1}{6\cdot16}+...+\dfrac{1}{104\cdot114}\)
\(=\dfrac{1}{10}\left(\dfrac{10}{5\cdot15}+\dfrac{10}{6\cdot16}+...+\dfrac{10}{104\cdot114}\right)\)
\(=\dfrac{1}{10}\left(\dfrac{1}{5}-\dfrac{1}{15}+\dfrac{1}{6}-\dfrac{1}{16}+...+\dfrac{1}{104}-\dfrac{1}{114}\right)\)
\(=\dfrac{1}{10}\left[\dfrac{1}{5}+\dfrac{1}{6}+...+\dfrac{1}{14}-\dfrac{1}{105}-\dfrac{1}{106}-...-\dfrac{1}{114}\right]\)
\(\left(\dfrac{1}{5\cdot105}+\dfrac{1}{6\cdot106}+...+\dfrac{1}{14\cdot114}\right)\cdot x=\dfrac{1}{5\cdot15}+\dfrac{1}{6\cdot16}+...+\dfrac{1}{104\cdot114}\)
=>\(\dfrac{1}{100}\left(\dfrac{1}{5}+\dfrac{1}{6}+...+\dfrac{1}{14}-\dfrac{1}{105}-\dfrac{1}{106}-...-\dfrac{1}{114}\right)\cdot x=\dfrac{1}{10}\cdot\left(\dfrac{1}{5}+\dfrac{1}{6}+...+\dfrac{1}{14}-\dfrac{1}{105}-\dfrac{1}{106}-...-\dfrac{1}{114}\right)\)
=>\(\dfrac{x}{100}=\dfrac{1}{10}\)
=>x=10