Các câu hỏi tương tự
Gọi z1; z2; z3; z4 là bốn nghiệm của phương trình ( z - 1 )( z + 2) ( z2 - 2z + 2) 0 trên tập số phức, tính tổng: A. 2/5 B. 3/5 C. 5/4 D. 6/7
Đọc tiếp
Gọi z1; z2; z3; z4 là bốn nghiệm của phương trình ( z - 1 )( z + 2) ( z2 - 2z + 2) = 0 trên tập số phức, tính tổng: 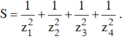
A. 2/5
B. 3/5
C. 5/4
D. 6/7
Cho phương trình: ( z2 - z) ( z + 3) (z + 2) = 10 .Tính tổng tất cả các phần thực của các nghiệm phương trình trên.
A. -1
B. -2
C. -3
D. -4
Gọi S là tổng các nghiệm phức của phương trình ( z - 1 ) 4 = 5. Tính S.
A. S = 0
B. S = 4
C. S = 2i
D. S = 4 5
Kí hiệu z1, z2 là hai nghiệm phức của phương trình
z
2
+
z
+
2
0
Tính
z
1
z
2
+
z
2
z
1
Đọc tiếp
Kí hiệu z1, z2 là hai nghiệm phức của phương trình z 2 + z + 2 = 0 Tính z 1 z 2 + z 2 z 1
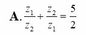
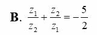
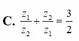
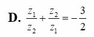
Kí hiệu
z
1
,
z
2
,
z
3
là ba nghiệm của phương trình phức
z
3
+
2
z
2
+
z
-
4
0
. Tính giá trị của biểu thức
T
z
1
+
z...
Đọc tiếp
Kí hiệu z 1 , z 2 , z 3 là ba nghiệm của phương trình phức z 3 + 2 z 2 + z - 4 = 0 . Tính giá trị của biểu thức T = z 1 + z 2 + z 3 .
![]()
![]()
![]()
![]()
Cho các số phức z thỏa mãn |z2 + 4| 2|z|. Kí hiệu M max|z| và m min|z|. Tìm module của số phức w M + m?
Đọc tiếp
Cho các số phức z thỏa mãn |z2 + 4| = 2|z|. Kí hiệu M = max|z| và m = min|z|. Tìm module của số phức w = M + m?
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn phương trình 4|z+i| + 3|z-i| = 10. Tính giá trị nhỏ nhất của |z|
A. 1 2
B. 5 7
C. 3 2
D. 1
Kí hiệu là hai nghiệm phức của phương trình
3
z
2
-
z
+
1
0
.Tính P
z
1
+
z
2
A
.
P
14
3...
Đọc tiếp
Kí hiệu là hai nghiệm phức của phương trình 3 z 2 - z + 1 = 0 .Tính P = z 1 + z 2
A . P = 14 3
B . P = 2 3
C . P = 3 3
D . P = 2 3 3
Số nghiệm của phương trình với ẩn số phức z: 4z2 + 8|z|2 - 3 = 0 là:
A. 3.
B. 2.
C. 4.
D. 1.
Kí hiệu
z
1
,
z
2
là hai nghiệm phức của phương trình
3
z
2
- z + 1 0. Tính P |
z
1
|+|
z
2
| A. P
3
3
B. P A. P
3
3
C. P...
Đọc tiếp
Kí hiệu z 1 , z 2 là hai nghiệm phức của phương trình 3 z 2 - z + 1 = 0. Tính P = | z 1 |+| z 2 |
A. P = 3 3
B. P = A. P = 3 3
C. P = 2 3
D. P = 14 3




