a) \(\sqrt{x-8}\) xác định khi
\(x-8\ge0\Leftrightarrow x\ge8\)
b) \(\sqrt{3x+1}\) xác định khi
\(3x+1\ge0\Leftrightarrow3x\ge-1\Leftrightarrow x\le-\dfrac{1}{3}\)
c) \(\sqrt{x^2+1}\)
Ta có: \(x^2\ge0\Rightarrow x^2+1\ge0\)
Vậy biểu thức được xác định với mọi x
d) \(\sqrt{\left(x-6\right)\left(x+3\right)}\)
Xác định khi
\(\left\{{}\begin{matrix}\left\{{}\begin{matrix}x-6\ge0\\x+3\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x-6< 0\\x+3\ge0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left\{{}\begin{matrix}x\ge6\\x\ge-3\end{matrix}\right.\\\left\{{}\begin{matrix}x< 6\\x< -3\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge6\\x< -3\end{matrix}\right.\)
e) \(\sqrt{\dfrac{-2}{x-5}}\) xác định khi
\(\left\{{}\begin{matrix}\dfrac{-2}{x-5}\ge0\\x-5\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le5\\x\ne5\end{matrix}\right.\)
\(\Leftrightarrow x< 5\)
f) \(\dfrac{4}{\sqrt{x+3}}\) xác định khi
\(x+3>0\)
\(\Leftrightarrow x>-3\)
g) \(\dfrac{6x-2}{\sqrt{x}-3}\)
Xác định khi:
\(\left\{{}\begin{matrix}\sqrt{x}\ge0\\\sqrt{x}-3\ne0\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x\ge0\\x\ne9\end{matrix}\right.\)
h) \(\sqrt{x^2-16}=\sqrt{\left(x+4\right)\left(x-4\right)}\)
Xác định khi
\(\left\{{}\begin{matrix}\left\{{}\begin{matrix}x+4< 0\\x-4< 0\end{matrix}\right.\\\left\{{}\begin{matrix}x+4\ge0\\x-4\ge0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left\{{}\begin{matrix}x< -4\\x< 4\end{matrix}\right.\\\left\{{}\begin{matrix}x\ge-4\\x\ge4\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x< -4\\x\ge4\end{matrix}\right.\)

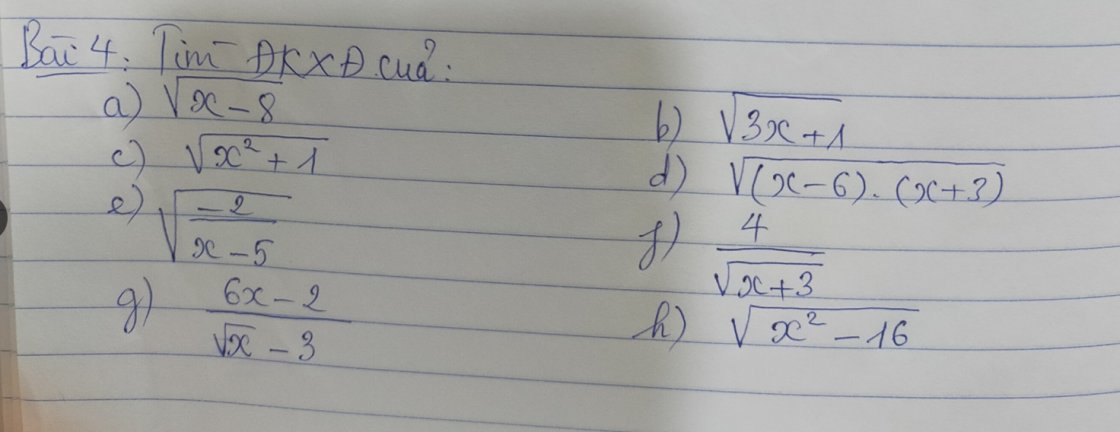




 không cần làm câu c đâu ạ, giúp e với nhaaa mn
không cần làm câu c đâu ạ, giúp e với nhaaa mn
 không cần làm hết đâu ạ chỉ cần 2,3 câu là đc ạ
không cần làm hết đâu ạ chỉ cần 2,3 câu là đc ạ