A. V=a3√36V=a336 B. V=a3√32V=a332C. V=a3√3V=a33 D. V=2a3√3
Các câu hỏi tương tự
Khối hộp đứng có diện tích xung quanh bằng 12a^2 , đáy ABCD là hình thoi có chu vi bằng 8a và góc BAD= ° 60 . Chiều cao và thể tích khối hộp lần lượt là
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, AB a,
B
A
D
^
60
0
,
S
O
⊥
A
B
C
D
và mặt phẳng (SCD) tạo với đáy một góc
60
0
. Tính thế tích khối chóp S.ABCD.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, AB = a, B A D ^ = 60 0 , S O ⊥ A B C D và mặt phẳng (SCD) tạo với đáy một góc 60 0 . Tính thế tích khối chóp S.ABCD.
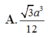
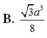
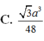
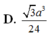
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a,
B
A
D
^
60
°
và SA vuông góc với mặt phẳng (ABCD). Góc giữa 2 mặt phẳng (SBD) và (ABCD) bằng 450. Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V1, khối đa diện còn lại có thể tích V2...
Đọc tiếp
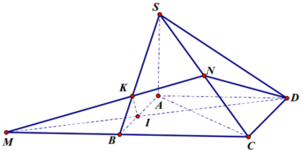
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, B A D ^ = 60 ° và SA vuông góc với mặt phẳng (ABCD). Góc giữa 2 mặt phẳng (SBD) và (ABCD) bằng 450. Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V1, khối đa diện còn lại có thể tích V2 (tham khảo hình vẽ bên). Tính tỉ số V 1 V 2
A. V 1 V 2 = 12 7
B. V 1 V 2 = 5 3
C. V 1 V 2 = 1 5
D. V 1 V 2 = 7 5
Cho khối chóp
S
.
A
B
C
D
có đáy
A
B
C
D
là hình thoi cạnh a góc
A
B
C
60
o
chiều cao bằng
3
a
thể tích của khối chóp bằng. A.
a
3
2
3
B. ...
Đọc tiếp
Cho khối chóp S . A B C D có đáy A B C D là hình thoi cạnh a góc A B C = 60 o chiều cao bằng 3 a thể tích của khối chóp bằng.
A. a 3 2 3
B. 3 a 2 3
C. a 3 2 12
D. a 3 3 2
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a và
B
D
C
⏜
60
0
, AB’ hợp với đáy (ABCD) một góc
30
0
. Thể tích của khối hộp là
Đọc tiếp
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a và B D C ⏜ = 60 0 , AB’ hợp với đáy (ABCD) một góc 30 0 . Thể tích của khối hộp là
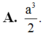
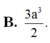
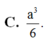
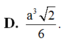
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a,
B
A
D
^
60
°
và SA vuông góc với mặt phẳng (ABCD). Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng
45
°
. Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích
V...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, B A D ^ = 60 ° và SA vuông góc với mặt phẳng (ABCD). Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng 45 ° . Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V 1 , khối đa diện còn lại có thể tích V 2 (tham khảo hình vẽ bên).
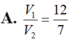
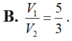
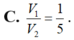
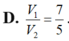
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2, cạnh bên SA vuông góc với đáy, góc giữa cạnh bên SC và đáy bằng 60°. Tính thể tích của khối trụ có một đáy là đường tròn ngoại tiếp hình vuông ABCD và chiều cao bằng chiều cao của khối chóp S.ABCD.
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2, cạnh bên SA vuông góc với đáy, góc giữa cạnh bên SC và đáy bằng 60°. Tính thể tích của khối trụ có một đáy là đường tròn ngoại tiếp hình vuông ABCD và chiều cao bằng chiều cao của khối chóp S.ABCD.
![]()
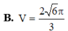
![]()
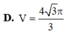
Cho khối hộp đứng có đáy là một hình thoi có độ dài đường chéo nhỏ bằng 10 và góc nhọn bằng
60
o
. Diện tích mỗi mặt bên của khối hộp bằng 10. Thể tích của khối hộp đã cho bằng A.
50
3
B. 50 C.
25
3
D.
100
3
Đọc tiếp
Cho khối hộp đứng có đáy là một hình thoi có độ dài đường chéo nhỏ bằng 10 và góc nhọn bằng 60 o . Diện tích mỗi mặt bên của khối hộp bằng 10. Thể tích của khối hộp đã cho bằng
A. 50 3
B. 50
C. 25 3
D. 100 3
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, B A D ^ = 120 ° , SA vuông góc với (ABCD). Gọi M, I lần lượt là trung điểm của BC và SB, góc giữa SM và (ABCD) bằng 60°. Khi đó thể tích của khối chóp I.ABCD bằng




