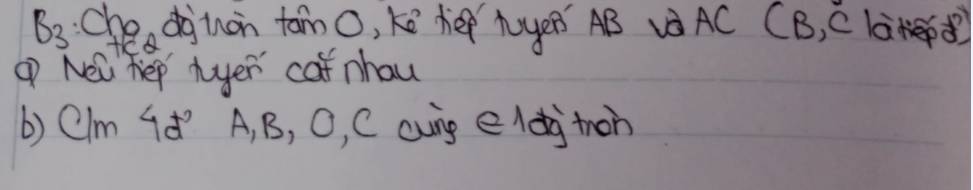kẻ hình nx nhé cám ưn nhìu 
1: Xét (O) có
ΔAHC nội tiếp
AC là đường kính
Do đó: ΔAHC vuông tại H
=>AH\(\perp\)HC tại H
=>AH\(\perp\)BC tại H
2: Ta có: ΔAHB vuông tại H
mà HM là đường trung tuyến
nên HM=AM=MB
Xét ΔOAM và ΔOHM có
OA=OH
AM=HM
OM chung
Do đó: ΔOAM=ΔOHM
=>\(\widehat{OAM}=\widehat{OHM}=90^0\)
=>MH là tiếp tuyến của (O)
3: Xét (O) có
\(\widehat{DCH}\) là góc nội tiếp chắn cung DH
\(\widehat{DAH}\) là góc nội tiếp chắn cung DH
Do đó; \(\widehat{DCH}=\widehat{DAH}\)
mà \(\widehat{DAH}=\widehat{DAC}\)(AD là phân giác của góc HAC)
nên \(\widehat{DCH}=\widehat{DAC}\)
Xét ΔDCE và ΔDAC có
\(\widehat{DCE}=\widehat{DAC}\)
\(\widehat{CDE}\) chung
Do đó: ΔDCE đồng dạng với ΔDAC
=>\(\dfrac{DC}{DA}=\dfrac{DE}{DC}\)
=>\(DC^2=DA\cdot DE\)
bài 2
giúp mik hai bài này với (kẻ bảng nx nha ) cảm ưn nhiều
kẻ cả hình nx 
kẻ hình nx nha
Vẽ e hình nx nhé
