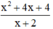Question

 Hơi loạn mong thông cảm

Giúp mk giải bài  này với mk dg cần gấp lắm

Cho phân thức 3x+3 phần x²-1

b rút gọn phân thức trên

C tìm x để phân thức có giá trị bằng -2

a tìm điều kiện của x để giá trị phân thức đc xác định

Answer 1

a, điều kiện xác định là \(x\ne1;x\ne-1\)

\(\frac{3x+3}{x^2-1}\)

\(=\frac{3\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\)

\(=\frac{3}{x-1}\)

b, để \(\frac{3x+3}{x^2-1}=-2\Rightarrow\frac{3}{x-1}=-2\)

\(\Rightarrow-2x+2=3\)

\(\Rightarrow-2x=1\)

\(\Rightarrow x=-\frac{1}{2}\)

Answer 2

a. ĐKXĐ: x² - 1\(\ne\)0 (=) x \(\ne\)\(\pm\)1

b. \(\frac{3x+3}{x^2-1}\)

\(=\frac{3\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\)

\(=\frac{3}{x+1}\)với x \(\pm\)1

c. \(\frac{3}{x+1}=-2\)

\(\Rightarrow\)\(\left(x+1\right).\left(-2\right)=3\)

\(-2x-2=3\)

\(-2x=5\)

\(x=-\frac{5}{2}\)(t/m đk)

Answer 3

Aww... Sr

Câu b và c phải như này cơ:

b. \(\frac{3x+3}{x^2-1}\)

\(=\frac{3\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\)

\(=\frac{3}{x-1}\)với x \(\ne\pm1\)

c. \(\frac{3}{x-1}=-2\Leftrightarrow\left(x-1\right).\left(-2\right)=3\)

\(-2x+2=3\)

\(-2x=1\)

\(x=-\frac{1}{2}\)với x \(\ne\pm1\)

Answer 4

Tl:

b.    \(\frac{3x+3}{x^2-1}=\frac{3\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\frac{3}{x-1}\)

c.    Cho pthức trên =-2

\(\Rightarrow\)\(\frac{3}{x-1}=-2\)

\(\Rightarrow-2\cdot\left(x-1\right)=3\)

\(\Rightarrow-2x+2=3\)

\(\Rightarrow x=\frac{-1}{2}\)

       Vậy ....

a.Pthức trên xác định\(\Leftrightarrow x-1\ne0\)

                                   \(\Leftrightarrow x\ne1\)

                                             Vậy ĐKXĐ:....
 

Answer 5

@❋ℳøøn sai rồi nha

\(\frac{3\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\)

rút gon đi phải bằng

\(\frac{3}{x-1}\)

Answer 6

Sửa lại r nha bn