Chọn D.
Phương pháp:
Đánh giá số nghiệm của phương trình bậc hai.
Cách giải:
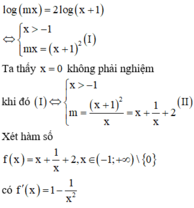
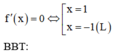
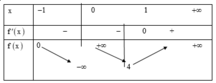
Dựa vào bảng biên thiên, ta có: phương trình đã cho có 1 nghiệm duy nhất

Chọn D.
Phương pháp:
Đánh giá số nghiệm của phương trình bậc hai.
Cách giải:
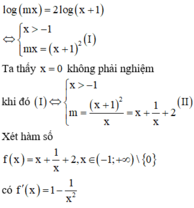
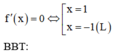

Dựa vào bảng biên thiên, ta có: phương trình đã cho có 1 nghiệm duy nhất

Có tất cả bao nhiêu số nguyên m để phương trình log ( m - x ) = 3 log ( 4 - 2 x - 3 ) có hai nghiệm thực phân biệt.
A. 6.
B. 2.
C. 3.
D. 5.
Có bao nhiêu giá trị m nguyên với m ∈ [ - 4 ; 4 ] để phương trình e x = m ( x + 1 ) có một nghiệm duy nhất?
A. 4.
B. 5.
C. 6.
D. 7.
Có bao nhiêu giá trị nguyên của tham số m để phương trình log 5 m x log 5 x + 1 = 2 có nghiệm duy nhất?
A. 1
B. 3
C. Vô số
D. 2
Cho phương trình 3 tan x + 1 sin x + 2 cos x = m s i n x + 3 cos x Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2018;2018] để phương trình trên có nghiệm duy nhất x ϵ (0;π/2) ?
A. 2018
B. 2015
C. 4036
D. 2016
Biết phương trình log 5 2 x + 1 x = 2 log 3 x 2 - 1 2 x có nghiệm duy nhất x = a + b 2 trong đó a, b là các số nguyên. Hỏi m thuộc khoảng nào dưới đây để hàm số y = m x + a - 2 x - m có giá trị lớn nhất trên đoạn [1;2] bằng -2.
A. m ∈ 2 ; 4
B. m ∈ 4 ; 6
C. m ∈ 6 ; 7
D. m ∈ 7 ; 9
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình log ( ( m - 1 ) . 16 x + 2 . 25 x 5 . 20 x ) - 5 x + 1 . 4 x = ( 1 - m ) 4 2 x - 2 . 25 x có hai nghiệm thực phân biệt. Số phần tử của S bằng
A. 4.
B. 3.
C. 1.
D. 2.
Biết rằng tập nghiệm S của bất phương trình log - x 2 + 100 x - 2400 < 2 có dạng S = a ; b \ x ∘ . Giá trị của a + b - x ∘ bằng:
A. 150.
B. 100.
C. 30.
D. 50.
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn - 5 ; 5 để phương trình e x = m x + 1 có nghiệm duy nhất?
A. 5
B. 6
C. 7
D. 10
Số giá trị nguyên dương của m để hàm số y = 1 3 x 3 - 3 x 2 + ( m - 2017 ) x + 2018 nghịch biến trên khoảng (0;2) là
A. 2015.
B. 2017.
C. 2016.
C. 2016.