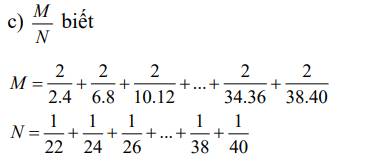\(M=\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{6}-\dfrac{1}{8}+...+\dfrac{1}{34}-\dfrac{1}{36}+\dfrac{1}{38}-\dfrac{1}{40}\)
\(M=\dfrac{1}{2}+\dfrac{1}{6}+...+\dfrac{1}{34}+\dfrac{1}{38}-\left(\dfrac{1}{4}+\dfrac{1}{8}+...+\dfrac{1}{36}+\dfrac{1}{40}\right)\)
Thêm bớt \(\dfrac{1}{4}+\dfrac{1}{8}+...+\dfrac{1}{36}+\dfrac{1}{40}\) vào tổng trên ta được:
\(M=\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{6}+...+\dfrac{1}{36}+\dfrac{1}{38}+\dfrac{1}{40}-2\left(\dfrac{1}{4}+\dfrac{1}{8}+...+\dfrac{1}{36}+\dfrac{1}{40}\right)\)
\(M=\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{36}+\dfrac{1}{38}+\dfrac{1}{40}-\left(\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{6}+...+\dfrac{1}{18}+\dfrac{1}{20}\right)\)
\(M=\dfrac{1}{22}+\dfrac{1}{24}+...+\dfrac{1}{38}+\dfrac{1}{40}=N\)
\(\Rightarrow\dfrac{M}{N}=1\)