Đáp án B
Hình nón có đường sinh l=2a và hợp với đáy góc 60 0 bán kính đáy là r = a
Vậy diện tích toàn phần cần tính là S = π r l + π r 2 = π . a .2 a + π a 2 = 3 π a 2
Đáp án B
Hình nón có đường sinh l=2a và hợp với đáy góc 60 0 bán kính đáy là r = a
Vậy diện tích toàn phần cần tính là S = π r l + π r 2 = π . a .2 a + π a 2 = 3 π a 2
Tìm góc α ∈ {π/6;π/4;π/3;π/2} để phương trình cos2x+ 3 sin2x-2cosx= 0 tương đương với phương trình c o s ( 2 x - α ) = cos x
A. α = π / 6
B. α = π / 4
C. α = π / 2
D. α = π / 3
Cho đồ thị hàm số y=1 + cosx (C) và y=1 + cos(x-α) (C') trên đoạn [ 0 ; π ] với 0 < α < π 2 . Tính α biết rằng diện tích hình phẳng giới hạn bởi (C) và (C') và đường x = 0 thì bằng diện tích hình phẳng giới hạn với(C') và đường y = 1, x = π . Ta được kết quả nào sau đây
A. α = π 6
B. α = π 4
C. α = π 3
D. α = π 12
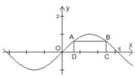
Cho hai điểm A, B thuộc đồ thị hàm số y = sinx trên đoạn [0;π], các điểm C, D thuộc trục Ox thỏa mãn ABCD là hình chữ nhật và CD = 2 π /3. Độ dài của cạnh BC bằng
A. 2 2
B. 1 2
C. 1
D. 3 2
Cho hình nón có thể tích bằng 12 π và diện tích xung quanh bằng 15. Tính bán kính đáy của hình nón biết bán kính là số nguyên dương.
A. 4
B. 3.
C. 6
D. 5
Cho sinα.cos(α+β) = sinβ với α+β ≠ π/2 + kπ,α ≠ π/2+lπ(k,l ϵ Z). Ta có:
A. tan(α+β)=2cotα
B. tan(α+β)=2cotβ
C. tan(α+β)=2tanβ
D.tan(α+β)=2tanα
Cho góc α thỏa mãn π < α < 3 π 2 và tan α = 2 : Tính giá trị của biểu thức A = sin 2 α + cos α + π 2
A. 4 + 2 5 10
B. 4 + 5 5 5
C. 4 + 2 5 5
D. 2 + 5 5
Cho hình trụ trục OO', đường tròn đáy (C) và (C'). Xét hình nón đỉnh O’, đáy (C) có đường sinh hợp với đáy góc a 0 o < a < 90 o . Cho biết tỉ số diện tích xung quanh của hình lăng trụ và hình nón bằng 3 . Tính giá trị a
A. 30 o
B. 45 o
C. 60 o
D. Kết quả khác
Cho hình nón có bán kính đáy bằng 2a và độ dài đường sinh l = 5 a 2 . Diện tích toàn phần của hình nón bằng
A. 10 πa 2
B. 11 πa 2
C. 3 πa 2
D. 9 πa 2
Cho hình nón có diện tích toàn phần bằng 5 π a 2 và bán kính đáy bằng a. Tính độ dài đường sinh l của hình nón đã cho
A. l = 5a.
B. l = 4a.
C. l = 2a.
D. l = 3a.