Chọn C.
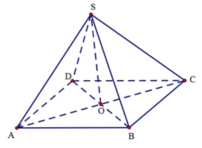
Gọi SO là đường cao của hình chóp tứ giác đều S.ABCD. Do đó góc giữa cạnh bên và mặt đáy là góc S B O ^
Ta có:
S O = h = a 2 ; O B = B D 2 = a 2
Tam giác vuông SBO tại O có SO=OB= a 2 nên cân tại O.
Suy ra S B O ^ = 45 o
Chọn C.

Gọi SO là đường cao của hình chóp tứ giác đều S.ABCD. Do đó góc giữa cạnh bên và mặt đáy là góc S B O ^
Ta có:
S O = h = a 2 ; O B = B D 2 = a 2
Tam giác vuông SBO tại O có SO=OB= a 2 nên cân tại O.
Suy ra S B O ^ = 45 o
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, chiều cao của chóp bằng a 3 2 . Góc giữa mặt bên và mặt đáy bằng
![]()
![]()
![]()
![]()
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng a 2 . Tính khoảng cách từ tâm O của đáy ABCD đến một mặt bên theo a.
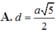
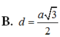
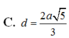

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, góc giữa mặt bên và mặt đáy bằng 60 ° . Tính theo a thể tích khối chóp S.ABCD
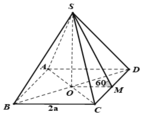
A. 4 a 3 3 3
B. a 3 3 3
C. 2 a 3 3 3
D. 2 a 3 6 3
Cho khối chóp tứ giác đều có độ dài cạnh đáy bằng 2 , chiều cao bằng 2 2 . Gọi O là tâm mặt cầu đường tròn ngoại tiếp khối chóp S.ABCD. Cosin góc giữa hai mặt phẳng (OAB) và (OCD) bằng:
![]()
![]()
![]()
![]()
Cho hình chóp tứ giác đều có cạnh đáy bằng a, mặt bên tạo với mặt đáy 1 góc 60 ° . Diện tích xung quanh của hình nón ngoại tiếp hình chóp là:
A. π a 2 10 4
B. π a 2 10 2
C. π a 2 5 2
D. π a 2 5 4
Cho hình chóp tứ giác đều có cạnh đáy bằng a và độ dài đường cao bằng a 14 2 .Tính tang của góc giữa cạnh bên và mặt đáy
A. 7
B. 14 2
C. 14
D. 7 2
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a, tâm O, SO=a (tham khảo hình vẽ bên). Khoảng cách từ O đến mặt phẳng (SCD) bằng
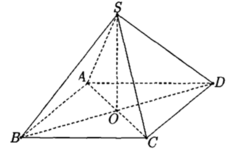
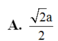
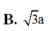
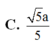
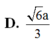
Một hình chóp tứ giác đều S.ABCD, đáy là hình vuông ABCD cạnh a; các mặt bên tạo với mặt đáy góc 60°. Tính độ dài l của cạnh bên hình chóp.
A. l = a 5 2
B. l = a 3 2
C. l = a 2 2
D. l = a 6 2
cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, SA vuông góc với mặt phẳng đáy, SA=BD=a√3. Góc giữa đường thẳng SC và mặt phẳng đáy (ABCD) bằng
A. 60° B. 30° C.90° D.45°