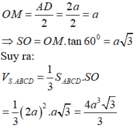
Đáp án A
Gọi O là tâm hình vuông ABCD, M là trung điểm CD.
Khi đó SO là đường cao hình chóp, góc SMO là góc giữa mặt bên và mặt đáy của hình chóp.
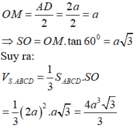
Cho hình chóp tam giác đều S.ABCD, cạnh đáy bằng a. Mặt bên tạo với mặt đáy một góc 60. Tính thể tích V của hình chóp S.ABCD. A)a³✓3/2 B)a³✓3/6 C)a³✓3/12 D)a³✓3/24
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 600. Tính thể tích khối chóp S.ABCD.
A. a 3 6
B. a 3 6 3
C. a 3 6 6
D. a 3 6 2
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a cạnh bên hợp với mặt đáy một góc 600. Tính theo a thể tích khối chóp S.ABCD.
A. V = 6 a 3 6
B. V = 6 a 3 2
C. V = 6 a 3 3
D. V = a 3 3
Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 60 0 . Tính thể tích của khối chóp S.ABCD theo a.
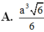
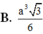
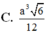
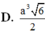
Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 600. Tính thể tích của khối chóp S.ABCD theo a .
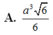
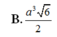
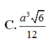
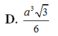
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a 3 , mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối chóp S.ABCD là:
A. 9 3 a 3 2
B. a 3 2
C. 3 a 3 3
D. 3 a 3 2
Cho hình chóp S.ABCD có SC ⊥ (ABCD), đáy ABCD là hình thoi có cạnh bằng a 3 và ABC ^ = 120 o . Biết rằng góc giữa hai mặt phẳng (SAB) và (ABCD) bằng 45°. Tính theo a thể tích khối chóp S.ABCD.
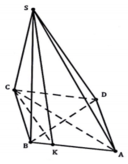
A. a 3 3 12
B. 3 a 3 3 12
C. a 3 3 4
D. 3 a 3 3 4
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a 2 , tam giác SAD cân tại S, mặt bên (SAD) vuông góc với mặt phẳng đáy. Biết thể tích S.ABCD bằng 4 a 3 /3. Tính khoảng cách h từ B đến mặt phẳng (SCD).
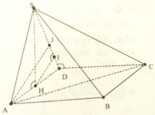
A. h = 2 3 a
B. h = 4 3 a
C. h = 8 3 a
D. h = 3 4 a
Cho hình chóp đều S.ABCD có cạnh đáy bằng a, biết góc giữa cạnh bên và mặt đáy bằng 45°. Tính thể tích V của khối chóp S.ABCD.
A. V = 2 6 a 3
B. V = 3 4 a 3
C. V = 3 12 a 3
D. V = 3 3 4 a 3
