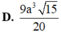Các câu hỏi tương tự
Xét khối chóp S.ABC có đáy ABC là tam giác vuông cân tại A, SA vuông góc với đáy, khoảng cách từ A đến mặt phẳng (SBC) bằng 3. Gọi
α
là góc giữa hai mặt phẳng (SBC) và (ABC), tính cos
α
khi thể tích khối chóp S.ABC nhỏ nhất.
Đọc tiếp
Xét khối chóp S.ABC có đáy ABC là tam giác vuông cân tại A, SA vuông góc với đáy, khoảng cách từ A đến mặt phẳng (SBC) bằng 3. Gọi α là góc giữa hai mặt phẳng (SBC) và (ABC), tính cos α khi thể tích khối chóp S.ABC nhỏ nhất.
![]()

![]()
Hình chóp S.ABC có SA, SB, SC đôi một vuông góc và SASBSC. Gọi
α
là góc giữa mặt (SAB) và (ABC). Tính cos
α
A. cos
α
1
2
B. cos
α
1
3
D. cos
α
1
6
D. cos
α
2
3
Đọc tiếp
Hình chóp S.ABC có SA, SB, SC đôi một vuông góc và SA=SB=SC. Gọi α là góc giữa mặt (SAB) và (ABC). Tính cos α
A. cos α = 1 2
B. cos α = 1 3
D. cos α = 1 6
D. cos α = 2 3
Cho lăng trụ đứng ABCABC có đáy ABC là tam giác cân, AB AC a, BAC
120
0
, BB a, I là trung điểm CC. Gọi
(
α
)
là góc giữa hai mặt phẳng (ABC) và (ABI). Tính cos
α
Đọc tiếp
Cho lăng trụ đứng ABCA'B'C' có đáy ABC là tam giác cân, AB = AC = a, BAC = 120 0 , BB' = a, I là trung điểm CC'. Gọi ( α ) là góc giữa hai mặt phẳng (ABC) và (AB'I). Tính cos α
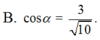
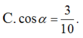
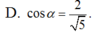
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với ABa, AD2a, SA2a và SA
⊥
(ABCD), Gọi a là góc giữa 2 đường thẳng SC và BD. Khi đó, cos
α
bằng
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=a, AD=2a, SA=2a và SA ⊥ (ABCD), Gọi a là góc giữa 2 đường thẳng SC và BD. Khi đó, cos α bằng
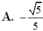
![]()
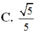
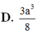
Cho hình chóp S.ABC có
S
A
⊥
(
A
B
C
)
, ACb, ABc,
B
A
C
^
α
. Gọi B, C lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính bán kính mặt cầu ngoại tiếp hình chóp A.BCCB theo b, c,
α
.
Đọc tiếp
Cho hình chóp S.ABC có S A ⊥ ( A B C ) , AC=b, AB=c, B A C ^ = α . Gọi B', C' lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính bán kính mặt cầu ngoại tiếp hình chóp A.BCC'B' theo b, c, α .
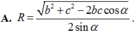
![]()
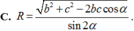
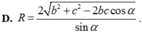
Cho hình chóp S.ABC có
S
A
⊥
m
p
(
A
B
C
)
,
S
A
4
α
5
,
A
B
A
C
α
,
B
C
6
α
5
. Gọi M là trung điểm của BC và
α
là góc g...
Đọc tiếp
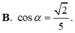
Cho hình chóp S.ABC có S A ⊥ m p ( A B C ) ,
S A = 4 α 5 ,
A B = A C = α , B C = 6 α 5 . Gọi M là trung điểm của BC và α là góc giữa hai đường thẳng AC, SM. Tính cos α
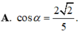
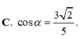
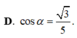
Cho hình chóp S.ABC có đáy ABC vuông cân tại B với AB a, SA
a
3
và
S
A
⊥
A
B
C
. Gọi M là điểm trên cạnh AB và AM x (0 x a), mặt phẳng
α
đi qua M và vuông góc với AB. Tìm x để diện tích thiết diện tạo bởi mặt phẳng
α
và hình chóp S.ABC lớn nhất
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC vuông cân tại B với AB = a, SA = a 3 và S A ⊥ A B C . Gọi M là điểm trên cạnh AB và AM = x (0 < x < a), mặt phẳng α đi qua M và vuông góc với AB. Tìm x để diện tích thiết diện tạo bởi mặt phẳng α và hình chóp S.ABC lớn nhất
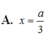

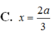
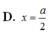
#SGD Bắc Giang – năm 2017 – 2018~Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật, ABa, BC a
3
, SAa và SA vuông góc với đáy ABCD. Tính sin α, với α là góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC).
Đọc tiếp
#SGD Bắc Giang – năm 2017 – 2018~Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật, AB=a, BC = a 3 , SA=a và SA vuông góc với đáy ABCD. Tính sin α, với α là góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC).
![]()
![]()
![]()
![]()
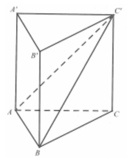
Cho hình lăng trụ đều ABC.A’B’C’. Biết khoảng cách từ điểm C đến mặt phẳng (ABC’) bằng a, góc giữa 2 mặt phẳng (ABC’) và (BCC’B’) bằng a với cos
α
1
3
(tham khảo hình vẽ dưới đây). Thể tích khối lăng trụ ABC.A’B’C’ bằng
Đọc tiếp
Cho hình lăng trụ đều ABC.A’B’C’. Biết khoảng cách từ điểm C
đến mặt phẳng (ABC’) bằng a, góc giữa 2 mặt phẳng (ABC’) và
(BCC’B’) bằng a với cos α = 1 3 (tham khảo hình vẽ dưới đây). Thể
tích khối lăng trụ ABC.A’B’C’ bằng