a) Điều kiện x>= -4
TH1 \(-4\le x< 0\)
\(< =>\sqrt{x+4}-x=x^2-x-4< =>\sqrt{x+4}=x^2-4\)
\(x+4=x^4-8x^2+16< =>x^4-8x^2-x+12=0< =>\left(-x^2-x+3\right)\left(-x^2+x+4\right)=0\)
\(\left[{}\begin{matrix}x=\dfrac{-1+\sqrt{13}}{2}\left(ktm\right)\\x=\dfrac{-1-\sqrt{13}}{2}\left(tm\right)\\x=\dfrac{1+\sqrt{17}}{2}\left(ktm\right)\\x=\dfrac{1-\sqrt{17}}{2}\left(ktm\right)x^2< 4\end{matrix}\right.\)
Th2 x\(\ge0\)
<=>\(\sqrt{x+4}=x^2-2x-4\)
\(< =>x+\sqrt{x+4}-x^2+x+4=0\)
\(x+\sqrt{x+4}+\left(x+\sqrt{x+4}\right)\left(\sqrt{x+4}-x\right)=0\)
\(< =>\left(x+\sqrt{x+4}\right)\left(\sqrt{x+4}-x+1\right)=0\)
\(< =>\left[{}\begin{matrix}x+\sqrt{x+4}>0\\\sqrt{x+4}=x-1< =>\left[{}\begin{matrix}x=\dfrac{3+\sqrt{21}}{2}\left(tm\right)\\x=\dfrac{3-\sqrt{21}}{2}\left(ktm\right)\end{matrix}\right.\end{matrix}\right.\)
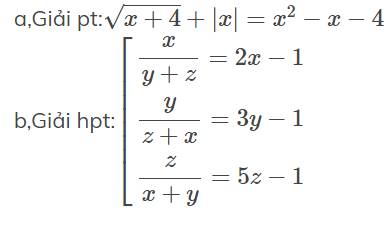
Help mik với
