c.
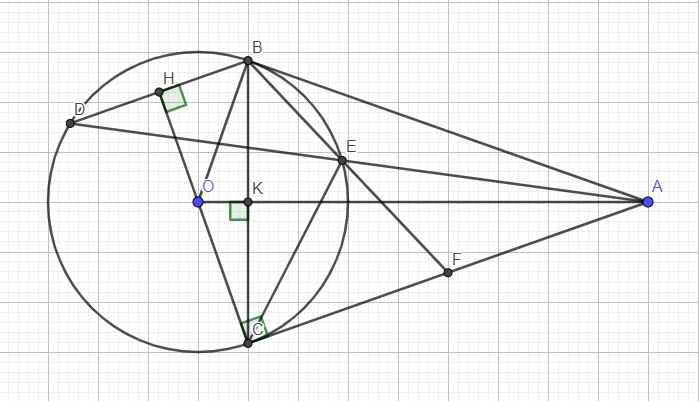
\(BD||AC\Rightarrow\widehat{BDE}=\widehat{EAF}\) (so le trong)
Mà \(\widehat{BDE}=\widehat{ABE}\) (cùng chắn BE)
\(\Rightarrow\widehat{EAF}=\widehat{ABE}\)
Hai tam giác AEF và BAF có: \(\left\{{}\begin{matrix}\widehat{AFE}\text{ chung}\\\widehat{EAF}=\widehat{ABE}\end{matrix}\right.\) \(\Rightarrow\Delta AEF\sim\Delta BAF\)
\(\Rightarrow\dfrac{AF}{BF}=\dfrac{EF}{AF}\Rightarrow AF^2=EF.BF\) (1)
Hai tam giác BCF và CEF có: \(\left\{{}\begin{matrix}\widehat{CFE}\text{ chung}\\\widehat{CBE}=\widehat{ECF}\left(\text{cùng chắn CE}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta BCF\sim\Delta CEF\Rightarrow\dfrac{BF}{CF}=\dfrac{CF}{EF}\Rightarrow CF^2=EF.BF\) (2)
(1);(2) \(\Rightarrow AF=CF\Rightarrow F\) là trung điểm AC
d.
Nối CO kéo dài cắt BD tại H
Do \(\left\{{}\begin{matrix}BD||AC\\OC\perp AC\end{matrix}\right.\) \(\Rightarrow OC\perp BD\Rightarrow H\) là trung điểm BD
\(\Rightarrow\Delta_VCHD=\Delta_VCHB\left(c.g.c\right)\Rightarrow S_{BCD}=2S_{CHB}\)
Gọi K là giao điểm AO và BC \(\Rightarrow\left\{{}\begin{matrix}BK=CK\\OK\perp BC\end{matrix}\right.\)
Hệ thức lượng trong tam giác vuông OAB:
\(OB^2=OK.OA\Rightarrow OK=\dfrac{OB^2}{OA}=\dfrac{R^2}{3R}=\dfrac{R}{3}\)
\(\Rightarrow BK=\sqrt{OB^2-OK^2}=\dfrac{2R\sqrt{2}}{3}\Rightarrow BC=2BK=\dfrac{4R\sqrt{2}}{3}\)
Hai tam giác vuông BHC và OKC đồng dạng (chung góc C) theo tỉ số đồng dạng \(k=\dfrac{BC}{OC}\)
\(\Rightarrow S_{BHC}=S_{OKC}.\left(\dfrac{BC}{OC}\right)^2=\dfrac{1}{2}.OK.KC.\left(\dfrac{BC}{OC}\right)^2=\dfrac{32\sqrt{2}}{81}R^2\)
\(\Rightarrow S_{BCD}=2S_{BHC}=\dfrac{64\sqrt{2}}{81}R^2\)





















 Help mik với
Help mik với