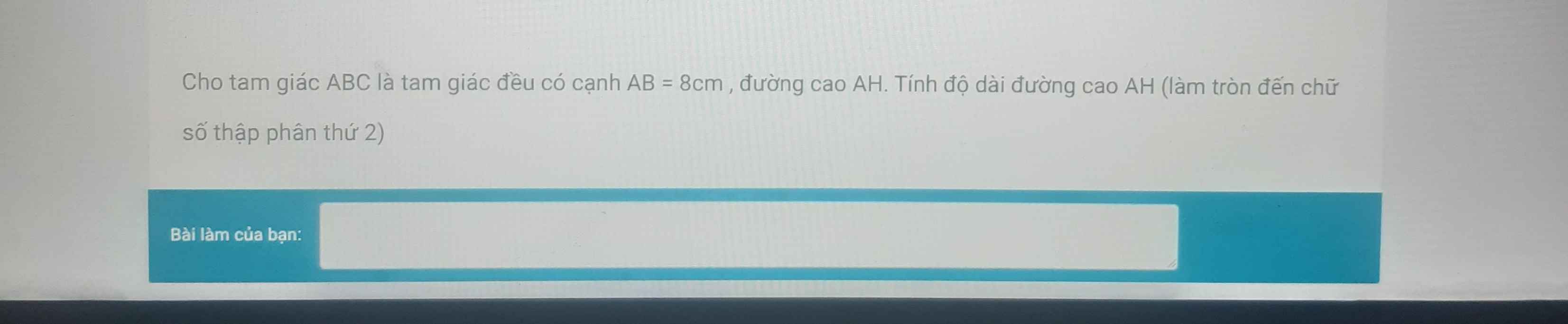
\(ĐKXĐ:x\le1.\)
\(\sqrt{x^2-3x-7}-\sqrt{1-x}=0.\\ \Leftrightarrow\sqrt{x^2-3x-7}=\sqrt{1-x}.\\ \Leftrightarrow x^2-3x-7=1-x.\\ \Leftrightarrow x^2-3x-7-1+x=0.\\ \Leftrightarrow x^2-2x-8=0.\\ \Leftrightarrow\left(x-4\right)\left(x+2\right)=0.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\left(koTM\right).\\x=-2\left(TM\right).\end{matrix}\right.\)
\(b;\sqrt{x+4\sqrt{x-4}}=5\Rightarrow x+4\sqrt{x-4}=25\Rightarrow4\sqrt{x-4}=25-x\Rightarrow16\left(x-4\right)=x^2-50x+625\Leftrightarrow\left[{}\begin{matrix}x=53\\x=13\end{matrix}\right.\)
thử lại vào pt thấy \(x=13\left(thỏa\right);x=53\left(loại\right)\)

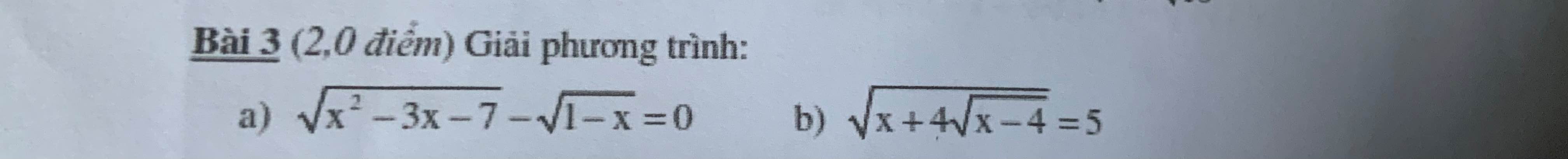 help
help








 help
help