Đáp án A
Phương pháp:
- Tìm TXĐ
- Tính đạo hàm
- Lập bảng xét dấu y’
- Xác định điểm cực đại và tính giá trị cực đại.
Cách giải:
Tập xác định: D = R
Hàm số đạt cực đại tại x = -1 và giá trị cực đại yCĐ = 2
Tìm giá trị của tham số m để hàm số
a) y = x 3 + (m + 3) x 2 + mx – 2 đạt cực tiểu tại x = 1
b) y = −( m 2 + 6m) x 3 /3 − 2m x 2 + 3x + 1 đạt cực đại tại x = -1;
Giá trị cực đại của hàm số y = x 3 − 3 x − 2 là
A. 0
B. 1
C. -1
D. 1
Cho hàm số y = x 3 - 3 x 2 + 1 . Tích các giá trị cực đại và giá trị cực tiểu của hàm số bằng
A. -6
B. -3
C. 0
D. 3
Cho hàm số y = x 3 - 3 x 2 - 2 . Gọi a,b lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số đó. Giá trị của 2 a 2 + b là:
A. -8.
B. -2
C. 2
D. 4
Tìm các giá trị của tham số m để đồ thị hàm số: y = x 3 - 3 x 2 - m x + 2 có điểm cực đại và điểm cực tiểu cách đều đường thẳng có phương trình: y = x - 1 ( d )
A. m = 0
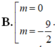
C. m = 2
D. m = - 9 2
Cho hàm số y = x 3 - 3 x 2 + 1 . Tích của giá trị cực đại và cực tiểu của hàm số bằng bao nhiêu?
A. -6
B. -3
C. 3
D. 4
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 3 x + m có giá trị cực đại và giá trị cực tiểu trái dấu.
A. m ∈ {-2;2}
B. m < -2 hoặc m > 2
C. -2 < m < 2
D. m ∈ R
Cho hàm số y = f(x) = x3 – 3x2 + m,∀m ∈ R. Tìm tham số m để hàm số có giá trị cực đại bằng 2
A. m = 2
B. m = -2
C. m = -4
D. m = 0
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 3 m x 2 + ( m - 1 ) x + 2 có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số có hoành độ dương
A. 0 ≤ m ≤ 1
B. m ≥ 1
C. m ≥ 0
D. m > 1
