Các câu hỏi tương tự
Gọi M, m tương ứng là giá trị lớn nhất và nhỏ nhất của hàm số y
sin
x
+
1
3
-
2
sin
x
. Khi đó ta có A. M + 2019m 2. B. M - 2019m -2019. C. 2M + 3m 0. D. M + m 1.
Đọc tiếp
Gọi M, m tương ứng là giá trị lớn nhất và nhỏ nhất của hàm số y = sin x + 1 3 - 2 sin x . Khi đó ta có
A. M + 2019m = 2.
B. M - 2019m = -2019.
C. 2M + 3m = 0.
D. M + m = 1.
Cho hàm số f(x)
x
-
1
2
a
x
2
+
4
a
x
-
a
+
b
-
2
, với a,b
∈
ℝ
. Biết trên khoảng...
Đọc tiếp
Cho hàm số f(x) = x - 1 2 a x 2 + 4 a x - a + b - 2 , với a,b ∈ ℝ . Biết trên khoảng - 4 3 ; 0 hàm số đạt giá trị lớn nhất tại x = -1. Hỏi trên đoạn - 2 ; - 5 4 , hàm số đạt giá trị nhỏ nhất tại giá trị nào của x?
A. x = - 5 4
B. x = - 4 3
C. x = - 3 2
D. x = -2
Gọi S là tập tất cả các giá trị nguyên của m để giá trị lớn nhất của hàm số y
sin
x
+
m
3
-
2
sin
x
thuộc đoạn [-2;2]. Khi đó số phần tử của S là A. 11 B. 10 C. Vô số D. 9
Đọc tiếp
Gọi S là tập tất cả các giá trị nguyên của m để giá trị lớn nhất của hàm số y = sin x + m 3 - 2 sin x thuộc đoạn [-2;2]. Khi đó số phần tử của S là
A. 11
B. 10
C. Vô số
D. 9
Cho hàm số y = \(|2x-x^2-\sqrt{\left(x+1\right)\left(3-x\right)}+b|\)Để giá trị lớn nhất của hàm số đạt giá trị nhỏ nhất thì giá trị của b thuộc khoảng nào
Cho hàm số y = f(x) có bảng xét dấu biến thiên như sau:
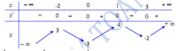
Giá trị lớn nhất của hàm số f(sin x - 1) bằng
A. 3
B. 3
C. -3
D. -2
Hàm số y = x 4 + a x 3 + b x 2 + 1 đạt giá trị nhỏ nhất tại x=0. Giá trị nhỏ nhất của biểu thức S= a + b là
A. 2
B. 0
C. -2
D. -1
Hàm số
y
4
-
x
-
x
+
6
đạt giá trị nhỏ nhất tại x x0. Tìm x0 A. x0 -6 B. x0 -1 C. x0 0 D. x0 4
Đọc tiếp
Hàm số y = 4 - x - x + 6 đạt giá trị nhỏ nhất tại x = x0. Tìm x0
A. x0 = -6
B. x0 = -1
C. x0 = 0
D. x0 = 4
Giá trị nhỏ nhất của hàm số
y
6
-
x
-
x
+
4
đạt tại x0, tìm x0? A. x0 -√10 B. x0 -4 C. x0 6 D. x0 √10
Đọc tiếp
Giá trị nhỏ nhất của hàm số y = 6 - x - x + 4 đạt tại x0, tìm x0?
A. x0 = -√10
B. x0 = -4
C. x0 = 6
D. x0 = √10
Hàm số
y
x
+
2
+
2
-
x
+
2
4
-
x
2
đạt giá trị lớn nhất, giá trị nhỏ nhất tại điểm có hoành độ là: A.
2
2
+
4
;
2
.
B.
2
2
-
2...
Đọc tiếp
Hàm số y = x + 2 + 2 - x + 2 4 - x 2 đạt giá trị lớn nhất, giá trị nhỏ nhất tại điểm có hoành độ là:
A. 2 2 + 4 ; 2 .
B. 2 2 - 2 ; 2 .
C. 2 2 ; 2 .
D. 4; 2
cho hàm số y = \(|2x-x^2-\sqrt{\left(x+1\right)\left(3-x\right)}+b|\) Để giá trị lớn nhất đạt giá trị nhỏ nhất thì giá trnàoị của b thuộc khoảng




