Chọn C
![]()
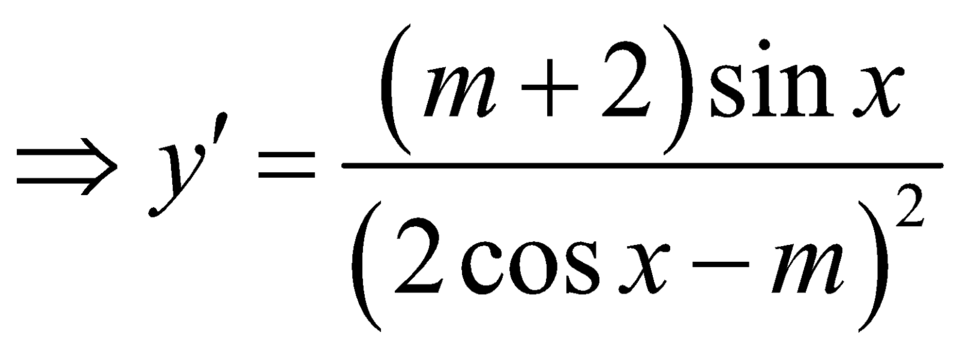 .
.
Vì ![]() nên hàm đồng biến trên
nên hàm đồng biến trên ![]() khi và chỉ khi:
khi và chỉ khi:
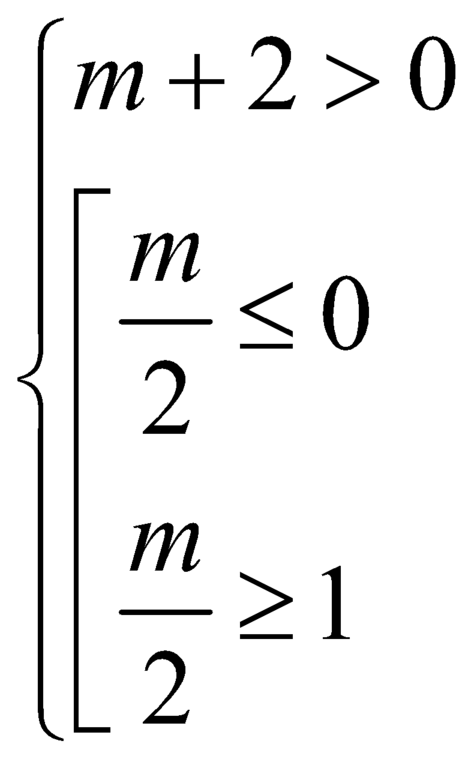
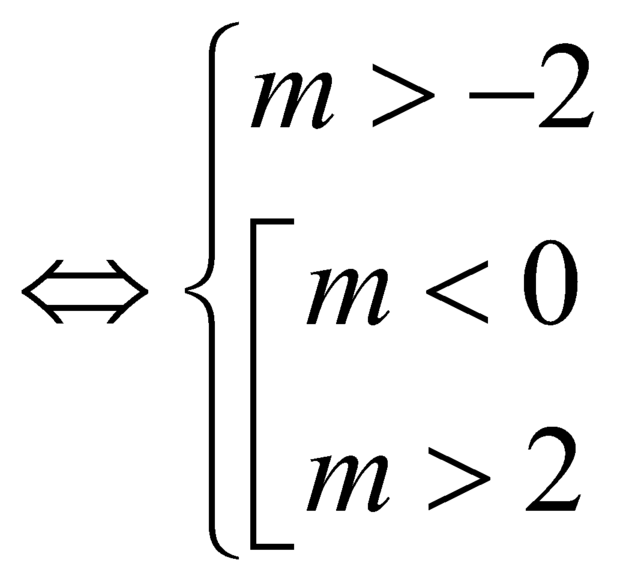
![]() .
.
Chọn C
![]()
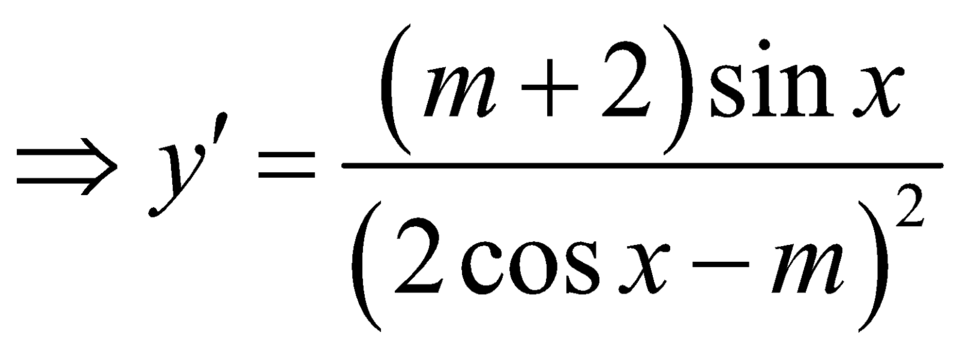 .
.
Vì ![]() nên hàm đồng biến trên
nên hàm đồng biến trên ![]() khi và chỉ khi:
khi và chỉ khi:
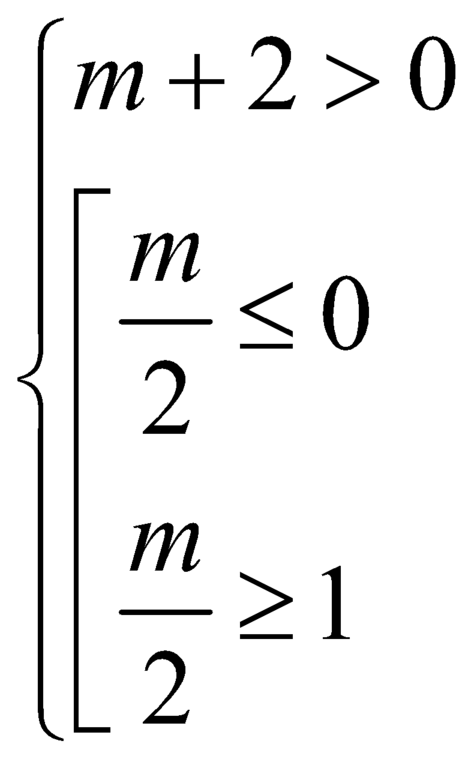
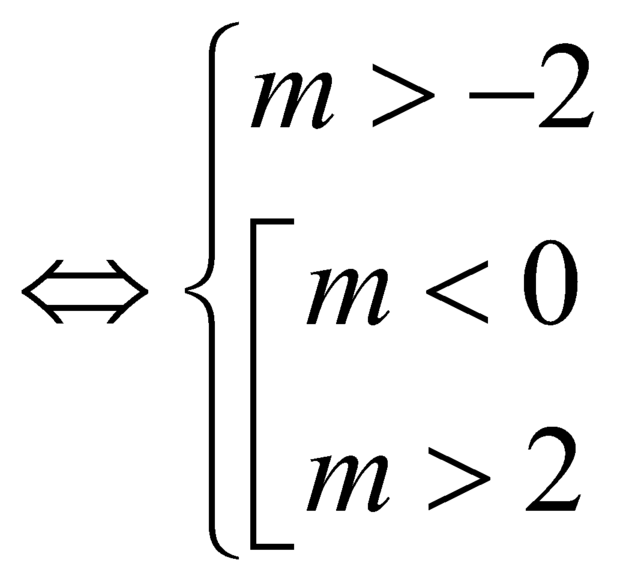
![]() .
.
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình bên. Phương trình f( 2 sin x) = m có đúng ba nghiệm phân biệt thuộc đoạn - π ; π khi và chỉ khi
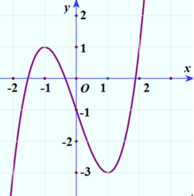
A. m ∈ - 3 ; 1
B. m ∈ - 3 ; 1
C. m ∈ [ - 3 ; 1 )
D. m ∈ ( - 3 ; 1 ]
Giá trị lớn nhất của hàm số f(x) = sin x + cos 2x trên [0; π ] là
A. 5 4
B. 1
C. 2
D. 9 8
Hàm số y = 2 x + m x 2 + 1 đồng biến trên khoảng 0 ; + ∞ khi và chỉ khi
A. m ≤ 0
B. m < 0
C. m ≤ 2
D. m < 2
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình bên. Phương trình f(2sin x) = m có đúng ba nghiệm phân biệt thuộc đoạn - π ; π khi và chỉ khi
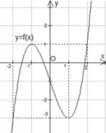
A. m ∈ - 3 ; 1
B. m ∈ - 3 ; 1
C. m ∈ [ - 3 ; 1 )
D. m ∈ ( - 3 ; 1 ]
1. Tìm m sao cho \(y=\frac{m\sin x+4}{\sin x+m}\)nghịch biến trên \(\left(0,\frac{\eta}{2}\right)\)
2. Tìm m sao cho \(y=\frac{\cos x+1}{m\cos x+2}\)nghịch biến trên \(\left(0,\frac{\eta}{2}\right)\)
Cho hàm số f x = a x 3 + b x 2 + c x + d với a , b , c , d là các hệ số thực và a ≠ 0 . Hàm số f x nghịch biến trên ℝ khi và chỉ khi:
A. a < 0 b 2 ≤ 3 a c
B. a < 0 b 2 < 3 a c
C. a > 0 b 2 ≥ 3 a c
D. a > 0 b 2 < 3 a c
cho y=1/3x³-(m-2)x²+(m²-3m+2)x+3. tìm m để a)Hàm số đồng biến với mọi x thuộc (2;dương vô cùng) b)Hàm số đồng biến với mọi x thuộc (trừ âm vô cùng;0) c)Hàm số nghịch biến với mọi x thuộc (-2;3)
Xét sự đồng biến, nghịch biến của các hàm số: y = x − sinx, x ∈ [0; 2 π ].
Có bao nhiêu giá trị nguyên của m ∈ ( - 15 ; 15 ) sao cho hàm số y = tan x - 10 tan x - m đồng biến trên khoảng 0 ; π / 4 ?
A. 20.
B. 9
C. 10.
D. 29.