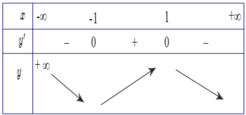
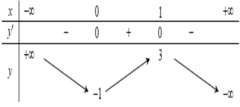
$y=|2x^2-3x-5|$
$y=\sqrt{(2x^2-3x-5)^2}$
$y'=\dfrac{(2x^2-3x-5).(4x-3)}{\sqrt{(2x^2-3x-5)^2}}$
$y'=\dfrac{(2x-5).(x+1).(4x-3)}{\sqrt{(2x^2-3x-5)^2}}$
Ta có Bảng Biến Thiên :
\begin{array}{|c|cc|} \hline x&-\infty&&-1&&\dfrac{3}{4}&&\dfrac{5}{2}&&\infty\\\hline y'&&-&||&+&0&-&||&+&\\\hline &&+\infty&&&\dfrac{49}{8}&&&&+\infty\\y&&\searrow&&\nearrow&&\searrow&&\nearrow\\&&&0&&&&0\\\hline\end{array}
Suy ra hàm số đồng biến trên các khoảng $(\dfrac{5}{2};+\infty)$ và $(-1;\dfrac{3}{4})$






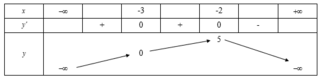
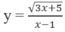 xác định trên R
xác định trên R