Các câu hỏi tương tự
Cho các mệnh đề :1) Hàm số yf(x) có đạo hàm tại điểm
x
0
thì nó liến tục tại
x
0
. 2) Hàm số yf(x) liên tục tại
x
0
thì nó có đạo hàm tại điểm
x
0
.3) Hàm số yf(x) liên tục trên đoạn [a;b] và f(a).f(b)0 thì phương trình f(x) có ít nhất một nghiệm trên khoảng (a;b).4) Hàm số yf(x) xác định trên đoạn [a;b] thì luôn tồn tại giá trị lớn nhất và giá trị n...
Đọc tiếp
Cho các mệnh đề :
1) Hàm số y=f(x) có đạo hàm tại điểm x 0 thì nó liến tục tại x 0 .
2) Hàm số y=f(x) liên tục tại x 0 thì nó có đạo hàm tại điểm x 0 .
3) Hàm số y=f(x) liên tục trên đoạn [a;b] và f(a).f(b)<0 thì phương trình f(x) có ít nhất một nghiệm trên khoảng (a;b).
4) Hàm số y=f(x) xác định trên đoạn [a;b] thì luôn tồn tại giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.
Số mệnh đề đúng là:
A. 2
B. 4
C. 3
D. 1
Cho hàm số
f
x
3
2
x
-
2
.
3
x
có đồ thị như hình vẽ sauCó bao nhiêu mệnh đề đúng trong các mệnh đề sau?(1) Đường thẳng y 0 cắt đồ thị hàm số (C) tại điểm có hoành độ là
x
log
3
2
(2) Bất phương trình
f
x
≥
-...
Đọc tiếp
Cho hàm số f x = 3 2 x - 2 . 3 x có đồ thị như hình vẽ sau
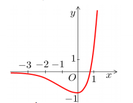
Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) Đường thẳng y = 0 cắt đồ thị hàm số (C) tại điểm có hoành độ là x = log 3 2
(2) Bất phương trình f x ≥ - 1 có nghiệm duy nhất.
(3) Bất phương trình f x ≥ 0 có tập nghiệm là - ∞ ; log 3 2
(4) Đường thẳng y = 0 cắt đồ thị hàm số (C) tại 2 điểm phân biệt.
A. 2
B. 4
C. 1
D. 3
Cho hàm số yf(x) có đồ thị đạo hàm yf’(x) được cho như hình vẽ bên và các mệnh đề sau:(1). Hàm số yf(x) có duy nhất 1 điểm cực trị(2). Hàm số yf(x) nghịch biến trên khoảng (-2;1) (3). Hàm số yf(x) đồng biến trên khoảng
0
;
+
∞
(4). Hàm số
g
x
f
x
+
x
2
có 2 điểm cực trị.Số mệnh đề đúng...
Đọc tiếp
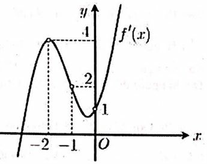
Cho hàm số y=f(x) có đồ thị đạo hàm y=f’(x) được cho như hình vẽ bên và các mệnh đề sau:
(1). Hàm số y=f(x) có duy nhất 1 điểm cực trị
(2). Hàm số y=f(x) nghịch biến trên khoảng (-2;1)
(3). Hàm số y=f(x) đồng biến trên khoảng 0 ; + ∞
(4). Hàm số g x = f x + x 2 có 2 điểm cực trị.
Số mệnh đề đúng là
A. 1
B. 3
C. 4
D. 2
Cho hàm số y f(x) liên tục trên khoảng
-
∞
;
+
∞
, thỏa mãn các điều kiện
l
i
m
x
→
0
f
x
x
2
và hàm số
y...
Đọc tiếp
Cho hàm số y = f(x) liên tục trên khoảng - ∞ ; + ∞ , thỏa mãn các điều kiện l i m x → 0 f x x = 2 và hàm số y = f 2 x sin 2 x k h i x > 0 a x + b k h i x ≤ 0 có đạo hàm tại điểm x = 0 Giá trị của biểu thức a + b bằng
A. 2
B. 3
C. 0
D. 1
Cho hàm số
f
x
3
2
x
−
2.3
x
có đồ thị như hình vẽ sauCó bao nhiêu mệnh đề đúng trong các mệnh đề sau?(1) Đường thẳng y0 cắt đồ thị hàm số (C) tại điểm có hoành độ là
x
log
3
2
(2) Bất phương trình
f
x
≥...
Đọc tiếp
Cho hàm số f x = 3 2 x − 2.3 x có đồ thị như hình vẽ sau
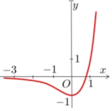
Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) Đường thẳng y=0 cắt đồ thị hàm số (C) tại điểm có hoành độ là
x
=
log
3
2
(2) Bất phương trình
f
x
≥
−
1
có nghiệm duy nhất.
(3) Bất phương trình
f
x
≥
0
có tập nghiệm là
−
∞
;
log
3
2
(4) Đường thẳng y=0 cát đồ thị hàm số (C) tại 2 điểm phân biệt
A. 2.
B. 4.
C. 1.
D. 3.
Cho hàm số
y
x
+
b
a
x
-
2
a
b
≠
-
2
. Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của đồ thị hàm số tại điểm A(1;-2) song song với đường thẳng
d
:
3
x
+
y...
Đọc tiếp
Cho hàm số y = x + b a x - 2 a b ≠ - 2 . Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của đồ thị hàm số tại điểm A(1;-2) song song với đường thẳng d : 3 x + y - 4 = 0 . Khi đó giá trị của a - 3b bằng
A. -2
B. 4
C. -1
D. 5
Cho hàm số
y
x
+
b
a
x
-
2
a
b
≠
-
2
. Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của đồ thị hàm số tại điểm A(1;-2) song song với đường thẳng
d
:
3
x
+...
Đọc tiếp
Cho hàm số y = x + b a x - 2 a b ≠ - 2 . Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của đồ thị hàm số tại điểm A(1;-2) song song với đường thẳng d : 3 x + y - 4 = 0 . Khi đó giá trị của a - 3 b bằng
A. -2
B. 4
C. -1
D. 5
Cho hàm số
y
x
+
b
a
x
−
2
a
b
≠
−
2
.
Biết rằng
a
v
à
b
là các giá tri thoả mãn tiếp tuyến của đồ thị hàm số tại điểm
M
...
Đọc tiếp
Cho hàm số y = x + b a x − 2 a b ≠ − 2 . Biết rằng a v à b là các giá tri thoả mãn tiếp tuyến của đồ thị hàm số tại điểm M 1 ; − 2 song song với đường thẳng d : 3 x + y − 4 = 0. Khi đó giá trị của bằng
A.2
B.0
C.-1
D.1
1. Cho hàm số y2x-1/x-1 . Lấy M thuộc C với XMm . tiếp tuyến của C tại M cắt 2 đường tiệm cận tại A,B . Gọi I là giao của 2 đường tiệm cận . CMR : M là trung điểm của AB và tam giác IAB có diện tích không phụ thuộc vào M 2.cho yx+2/x-3 tìm M thuộc C sao cho khoảng cách từ M đến 2 đường tiệm cận C bằng nhau 3. cho y x+2/x-2 tìm M thuộc C sao cho M cách đều hai trục tọa độ . viết pttt của C biết tiếp tuyến đó đi qua A(-6;5) 4 . cho y x+1/x-1 . CMR (d) : 2x-y+m0 luôn cắt C tại A,B trên 2 nhánh củ...
Đọc tiếp
1. Cho hàm số y=2x-1/x-1 . Lấy M thuộc C với XM=m . tiếp tuyến của C tại M cắt 2 đường tiệm cận tại A,B . Gọi I là giao của 2 đường tiệm cận . CMR : M là trung điểm của AB và tam giác IAB có diện tích không phụ thuộc vào M
2.cho y=x+2/x-3 tìm M thuộc C sao cho khoảng cách từ M đến 2 đường tiệm cận C bằng nhau
3. cho y = x+2/x-2 tìm M thuộc C sao cho M cách đều hai trục tọa độ . viết pttt của C biết tiếp tuyến đó đi qua A(-6;5)
4 . cho y = x+1/x-1 . CMR (d) : 2x-y+m=0 luôn cắt C tại A,B trên 2 nhánh của (C) . tìm m để AB ngắn nhất





