Gọi m' là khối lượng của nhôm và chì
Ta có V= \(m \over D\).
=> V nhôm = \(\frac{m'}{2.7}\)
=> V chì = \(\frac{m'}{11.3}\)
vì \(\frac{m'}{2.7}>\frac{m'}{11.3}\)
nên V nhôm > V chì
Một bình đựng nước dạng hình nón (không có đáy), đựng đầy nước. Người ta thả vào đó một khối cầu không thấm nước, có đường kính bằng chiều cao của bình nước và đo được thể tích nước tràn ra ngoài là V. Biết rằng khối cầu tiếp xúc với tất cả các đường sinh của hình nón và đúng một nửa của khối cầu chìm trong nước (hình bên).
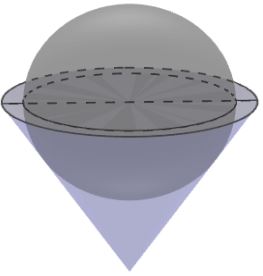
Tính thể tích nước còn lại trong bình.
A. 1 6 V
B. 1 3 V .
C. V
D. 1 π V .
Cho hình trụ có hai đường tròn đáy lần lượt là (O); (O’). Biết thể tích khối nón có đỉnh là O và đáy là hình tròn (O’) là a 3 , tính thể tích khối trụ đã cho ?
A. 2 a 3
B. 4 a 3
C. 6 a 3
D. 3 a 3
Gọi (S ) là khối cầu bán kính r(n) là khối nón có bán kính đáy R và chiều cao h. Biết rằng thể tích của khối cầu (S) và khối nón (N) bằng nhau, tính tỉ số h R .
A. 1
B. 4/3
C. 12
D. 4
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a a > 0 . Hai mặt phẳng (SBC) và S C D cùng tạo với mặt phẳng (ABCD) một góc 45 ° . Biết S B = a và hình chiếu của S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính thể tích khối chóp S.ABCD
A. 2 a 3 3
B. 2 a 3 6
C. a 3 4
D. 2 a 3 9
Sự tăng trưởng của một loài vi khuẩn được tính theo công thức S = A . e x , trong đó A là số lượng vi khuẩn ban đầu, r là tỉ lệ tăng trưởng (r < 0), t là thời gian tăng trưởng. Biết rằng số lượng vi khuẩn ban đầu là 150 con và sau 5 giờ có 450 con, tìm số lượng vi khuẩn sau 10 giờ tăng trưởng.
A. 900
B. 1350
C. 1050
D. 1200
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2 2 , cạnh bên SA vuông góc với mặt phẳng đáy và SA=3 Mặt phẳng α qua A và vuông góc với SC cắt các cạnh SB, SC, SD lần lượt tại các điểm M, N, P. Tính thể tích V của khối cầu ngoại tiếp tự diện CMNP.
A. V = 64 2 π 3
B. V = 125 π 6
C. V = 32 π 3
D. V = 10 Sπ 3
Cho hình vuông ABCD cạnh 4a. Trên cạnh AB và AD lần lượt lấy hai điểm H và K sao cho BH = 3HA và AK = 3KD. Trên đường thẳng vuông góc tại H lấy điểm S sao cho S B H ^ = 30 ∘ . Gọi E là giao điểm của CH và BK. Tính thể tích của khối cầu ngoại tiếp của hình chóp SAHEK.
A. 52 a 3 13 3
B. 52 a 3 12 3
C. a 3 13 3
D. 54 a 3 13 3
một hình lập phương đc tạo bởi 8 khối gỗ hình lập phương cạnh 1cm và 1 hình lập phương nữa đc tạo bởi 27 khối gỗ hình lập phương có cạnh là 1cm. Hỏi có thể xếp tất cả các khối gỗ của 2 hình lập phương thành 1 hình lập phương mới ko
Cho p và q là các số nguyên tố lớn hơn 3 và thỏa mãn p=q+2. Khi đó số dư của p+q chia 12 là?
