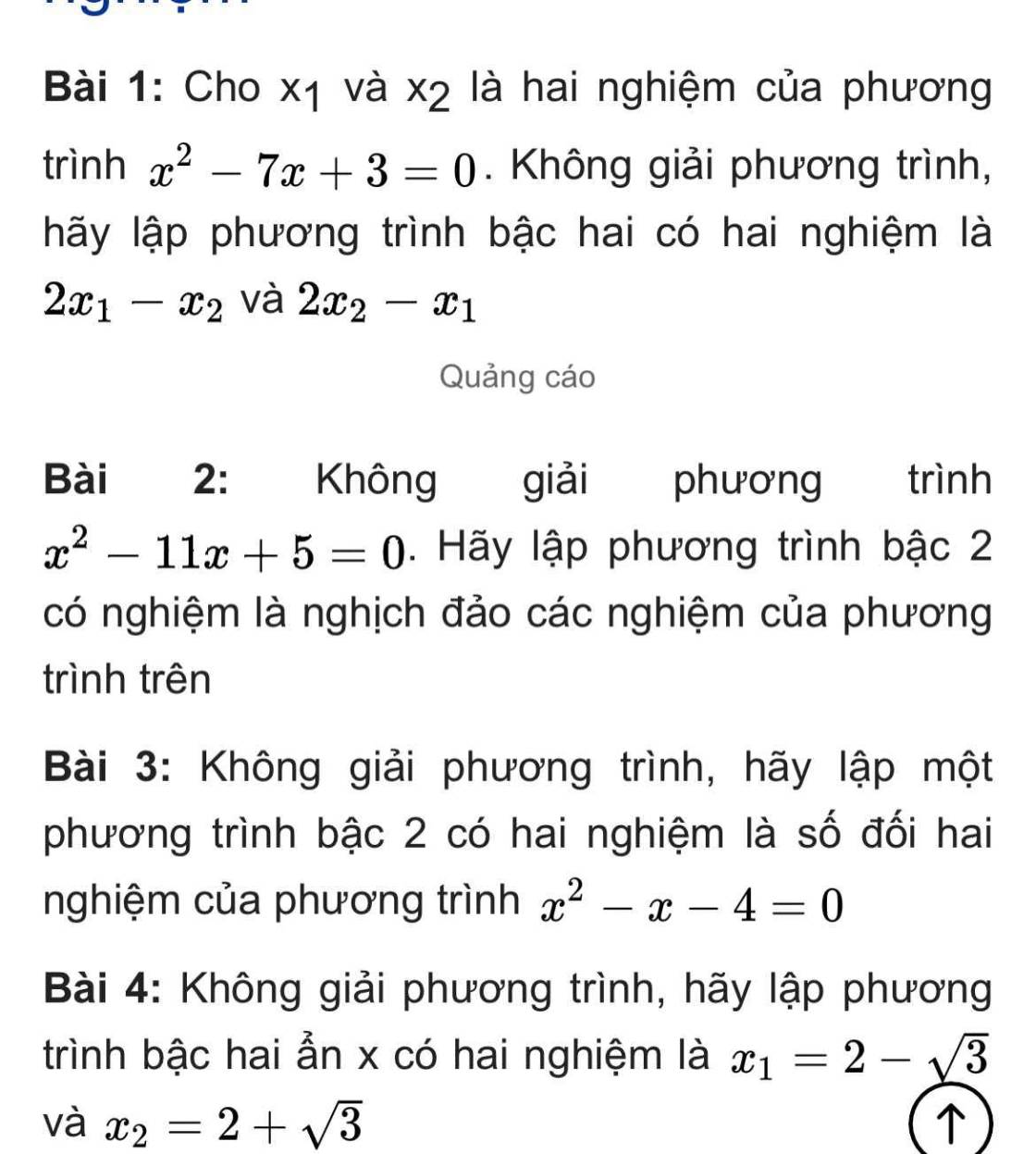
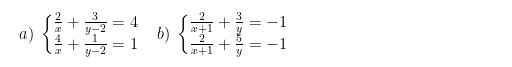bài 4:
\(x_1+x_2=2-\sqrt{3}+2+\sqrt{3}=4\)
\(x_1\cdot x_2=\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)=4-3=1\)
Phương trình bậc hai lập được là \(y^2-4y+1=0\)
bài 3:
\(x_1+x_2=-\dfrac{b}{a}=1;x_1x_2=\dfrac{c}{a}=-4\)
\(\Leftrightarrow-x_1+\left(-x_2\right)=-1;\left(-x_1\right)\cdot\left(-x_2\right)=\left(-1\right)\cdot\left(-1\right)\cdot\left(-4\right)=-4\)
Phương trình bậc hai lập được là
\(a^2+a-4=0\)
Bài 2:
\(x^2-11x+5=0\)
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=11\\x_1x_2=\dfrac{c}{a}=5\end{matrix}\right.\)
\(\dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{x_1+x_2}{x_1x_2}=\dfrac{11}{5};\dfrac{1}{x_1}\cdot\dfrac{1}{x_2}=\dfrac{1}{x_1x_2}=\dfrac{1}{5}\)
Phương trình bậc hai lập được là:
\(a^2-\dfrac{11}{5}a+\dfrac{1}{5}=0\)
Bài 1:
Theo Vi-et, ta có:
\(x_1+x_2=-\dfrac{b}{a}=7;x_1x_2=\dfrac{c}{a}=3\)
\(\left(2x_1-x_2\right)\left(2x_2-x_1\right)\)
\(=4x_1x_2-2\left(x_1^2+x_2^2\right)+x_1x_2\)
\(=-2\left[\left(x_1+x_2\right)^2-2x_1x_2\right]+5x_1x_2\)
\(=-2\left(x_1+x_2\right)^2+9x_1x_2\)
\(=-2\cdot7^2+9\cdot3=-2\cdot49+27=-98+27=-71\)