\(\left(\dfrac{x-1}{\sqrt{x^2+1}}\right)'=\dfrac{\left(x-1\right)'\cdot\sqrt{x^2+1}-\left(x-1\right)\cdot\left(\sqrt{x^2+1}\right)'}{\left(\sqrt{x^2+1}\right)^2}\)
\(=\dfrac{\sqrt{x^2+1}-\left(x-1\right)\cdot\dfrac{\left(x^2+1\right)'}{2\sqrt{x^2+1}}}{x^2+1}\)
\(=\dfrac{\sqrt{x^2+1}-\left(x-1\right)\cdot\dfrac{2x}{2\sqrt{x^2+1}}}{\left(x^2+1\right)}\)
\(=\dfrac{\sqrt{x^2+1}-\left(x-1\right)\cdot\dfrac{x}{\sqrt{x^2+1}}}{x^2+1}=\dfrac{x^2+1-x\left(x-1\right)}{\left(x^2+1\right)\cdot\sqrt{x^2+1}}\)
\(=\dfrac{x^2+1-x^2+x}{\left(x^2+1\right)\cdot\sqrt{x^2+1}}=\dfrac{x+1}{\left(x^2+1\right)\left(\sqrt{x^2+1}\right)}\)
=>a=1;b=1
=>a+3b=4
=>Chọn C






 Giúp em với ạ. Cần rất gấp ạ. Em cảm ơn ạ
Giúp em với ạ. Cần rất gấp ạ. Em cảm ơn ạ








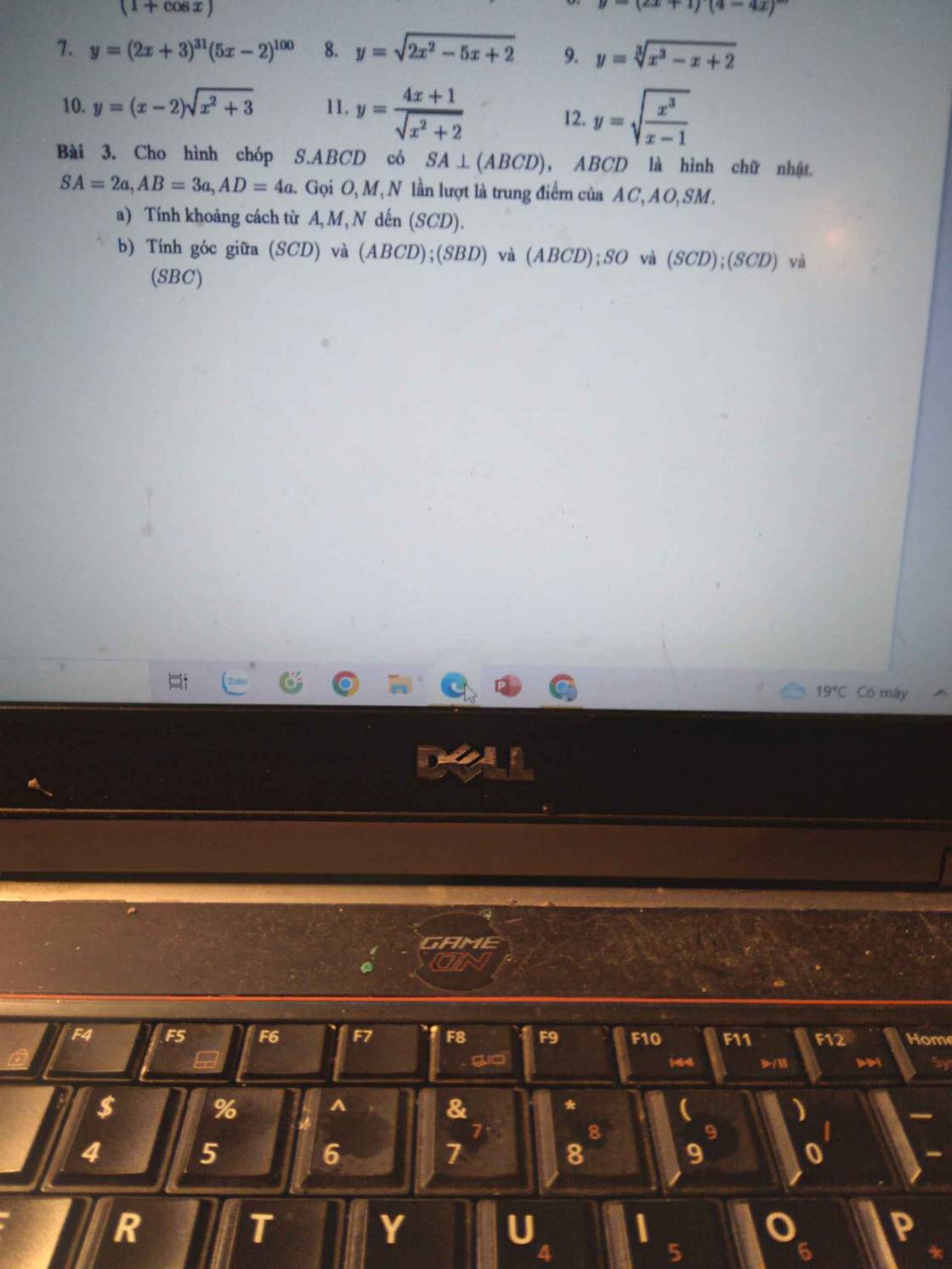 Giúp em bài 3 với ạ. Em cảm ơn ạ
Giúp em bài 3 với ạ. Em cảm ơn ạ




