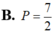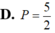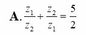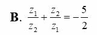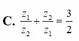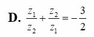Question

Gọi z1, z2 là 2 nghiệm phức của phương trình z²-4z+8=0 thì |z1|+|z2|-|z1z2| bằng bao nhiêu?

Answer 1

\(z^2-4z+8=0\)

=>\(\left(z-2\right)^2=-4\)

=>\(\left[{}\begin{matrix}z=-2i+2\\z=-2i-2\end{matrix}\right.\)

\(\left|z_1\right|+\left|z_2\right|-\left|z_1\cdot z_2\right|\)

\(=\left|-2i+2\right|+\left|-2i-2\right|-\left|\left(-2i+2\right)\left(-2i-2\right)\right|\)

\(=\sqrt{\left(-2\right)^2+2^2}++\sqrt{\left(-2\right)^2+\left(-2\right)^2}-\left|4i^2-4\right|\)

\(=\sqrt{8}+\sqrt{8}-\left|-8\right|=4\sqrt{2}-8\)